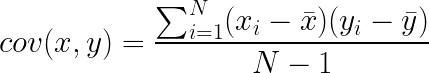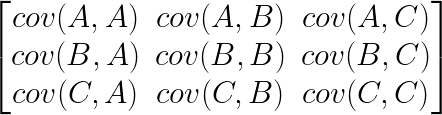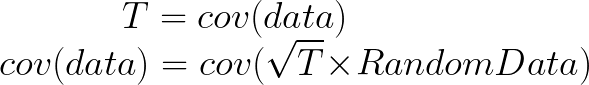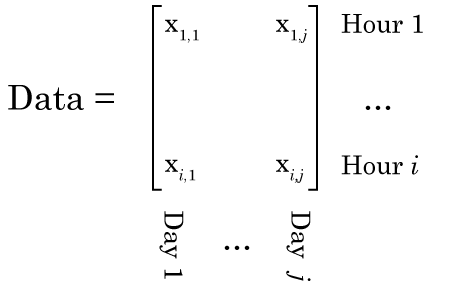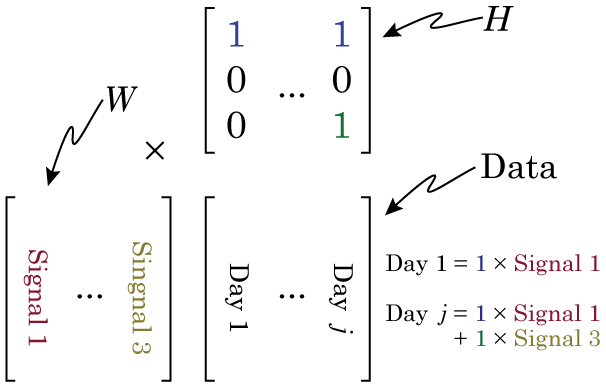The first rule of optimization is: Don’t do it.
The second rule of optimization (for experts only) is: Don’t do it yet.
These rules exist because, in general, if you try to rewrite your code to get a speed up, you will probably waste a lot of time and end up with code that is unreadable, fragile and that only runs a few milliseconds faster. This is especially true in scientific computing, where we are writing in high level languages, which use highly optimized libraries to perform computationally intensive tasks.
However, there are times when those rules of optimization can be broken. And there is a super simple way of leveraging parallel programming in Python that can give you a >10x speed up.
We all know that when we are writing code in numpy, we want to used vectorized code. So if we wanted to add 2 to every element in a vector we would never write:
import numpy as np
vector = np.array([1,2,3])
new_vector = np.zeros_like(vector)
for n in range(vector.size):
new_vector[n] = vector[n] + 2We would instead write:
new_vector = vector + 2In fact we can see that the vectorized approach is not only much simpler, but much faster. Using a for loop takes 300 ms:
import time
array_size = 1000000
vector = np.arange(array_size)
time0 = time.time()
new_vector = np.zeros_like(vector)
for n in range(vector.size):
new_vector[n] = vector[n]+2
time1 = time.time()
print(time1-time0) #About 300 msWhile the vectorized edition takes 1 ms.
vector = np.arange(array_size)
time0 = time.time()
new_vector = vector+2
time1 = time.time()
print(time1-time0) #About 1 msBut you don’t have to be a veteran coder to experience situations where you CAN’T vectorize the code. In my example we’re going to imagine we have a 3D matrix that represents video data, of shape (n_frames, n_rows, n_cols).
Imagine that each frame needs to be subjected to a function in an image processing library, and this is very computationally expensive. A lot of people would write code very much like the non-vectorized code above. We would know that this code is bad, but there was nothing we could do., e.g.
img_stack = np.random.random((100,512,512)) #My fake image stack
def expensive_function(input):
time.sleep(0.1) #fake computationally expensive task
return input
time0 = time.time()
output = np.zeros_like(img_stack)
for f in range(img_stack.shape[0]):
output[f,:,:] = expensive_function(img_stack[f,:,:])
time1 = time.time()
print(time1-time0) #Just over 10 seconds.The trick
So we want to do this task in parallel. The processing of each frame is completely independent of the others, so if we could only get each core in the CPU to do a selection of the frames, we could speed this process up a lot.
But a lot of people are scared of parallel processing. They think it is always a nightmare of workers, queues and stacks and a mess of synchronization, thread locks and deadlocks. But let me show you how do it easily. First we import the multiprocessing library, and figure out how many cores are available:
import multiprocessing
num_processes = multiprocessing.cpu_count()Then we split our data up so that each chunk we want to process independently is it’s own element in an array:
chunks = [img_stack[f, :, :] for f in range(img_stack.shape[0])]And then we pass each chunk to our function in parallel with this magical code:
with multiprocessing.Pool(processes=num_processes) as pool:
results = pool.map(expensive_function, chunks)Now, that code will work without any changes in an IPython notebook. If you are running the code directly, you need to hide the Pool() call within another function [this is due to the vagaries of how the multiprocessing library works, discussed below). But a minimal version looks like this:
img_stack = np.random.random((100,512,512)) #My fake image stack
chunks = [img_stack[f, :, :] for f in range(img_stack.shape[0])]
def expensive_function(input):
time.sleep(0.1) #fake computationally expensive task
return input
def run():
num_processes = multiprocessing.cpu_count()
with multiprocessing.Pool(processes=num_processes) as pool:
results = pool.map(expensive_function, chunks)
return results
if __name__ == "__main__":
results = np.array(run())So that is wonderfully simple. But you might have one worry. Synchronizing across threads in notoriously difficult. Am I sure that the processed frames are returned in the same order they were put in? Yes I am sure. Check this out. First we make an numpy array with values that make it easy to track:
n_frames = 100
arr = np.arange(n_frames).reshape((n_frames,1,1))
print(arr)
array([[[ 0]],
[[ 1]],
...
[[98]],
[[99]]])Then we pass that array in like before
chunks = [arr[f, :, :] for f in range(arr.shape[0])]
def expensive_function(input):
time.sleep(0.1) #fake computationally expensive task
return input
def run():
num_processes = multiprocessing.cpu_count()
with multiprocessing.Pool(processes=num_processes) as pool:
results = pool.map(expensive_function, chunks)
return results
if __name__ == "__main__":
results = np.array(run())
And if you look at the end, your results will all be perfectly in order.
I will finally give you a little warning, and it relates to why the function needs to be hidden behind a if __name__ == “__main__”. The multiprocessing library generally works letting each CPU load your whole script before it runs. So if any functions are called ‘out in the open’, the will be called when the script is loaded. And if those functions make a call to multiprocessing.Pool() then they will all spawn new processes, and each of those processes will spawn new processes, and so on. So you do need to be a little careful. But so long as you make sure all your code is compartmentalized in functions, and your entry into the Pool() function is hidden behind a if __name__ condition, this is an easy way to get a big speed boost. Similarity, don’t just dump your whole code into this pool.map() function. You don’t want to accidentally parallelize loading your data into RAM. But if your data is sitting nicely in memory, and you’re iterating through it, consider the multiprocessing.Pool() approach.
]]>Seems reasonable right? Well it’s not reasonable. In fact, it’s even less reasonable than I thought.
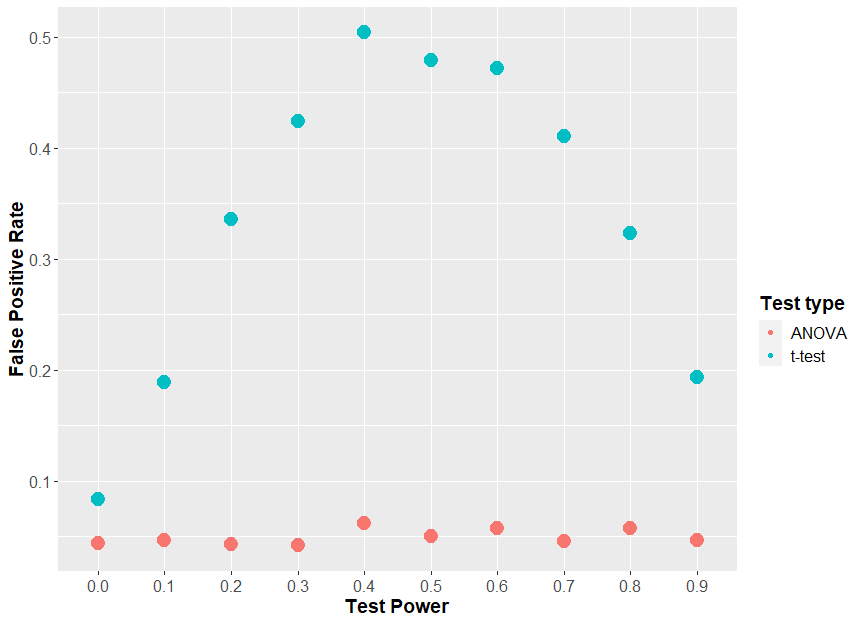
If you believe the approach above is reasonable, I think If I show you a graph that could be generated in the above situation you’ll start to see the problem

One way to frame the logical flaw lies that underpins this problem is that it is a mistake to conclude that if p > 0.05, then that means the drug has had no effect. When p = 0.06, it means that if the null hypothesis was true, we would get a t value as, or more, extreme in 6/100 trials. This is not the same thing as saying there is no effect of the drug. Another way to think about it is that we can’t conclude anything about the difference in the effect of the drug in males and females, because we never actually compared it.
Perhaps you say “You’ve picked some specific case where the ‘two t-test’ approach doesn’t work, and okay, I get that some anally retentive statistician may have a problem with this approach, but it can’t be that bad’. Well it is. At worst, this approach will give you a false answer 50% of the time! Let me show you.
If we generate data just like the above, where there is no true effect of sex, and we keep everything constant, apart from an increasing effect of our “drug”, we can look to see how often sex appears to have a statistically significant effect (i.e. the two t-tests give different results, one significant, one insignificant). How frequently this happens could be called the “false positive rate”. When we do that, we see that at a maximum, 50% of the time the two t-test approach tells us sex has an effect when there was none.
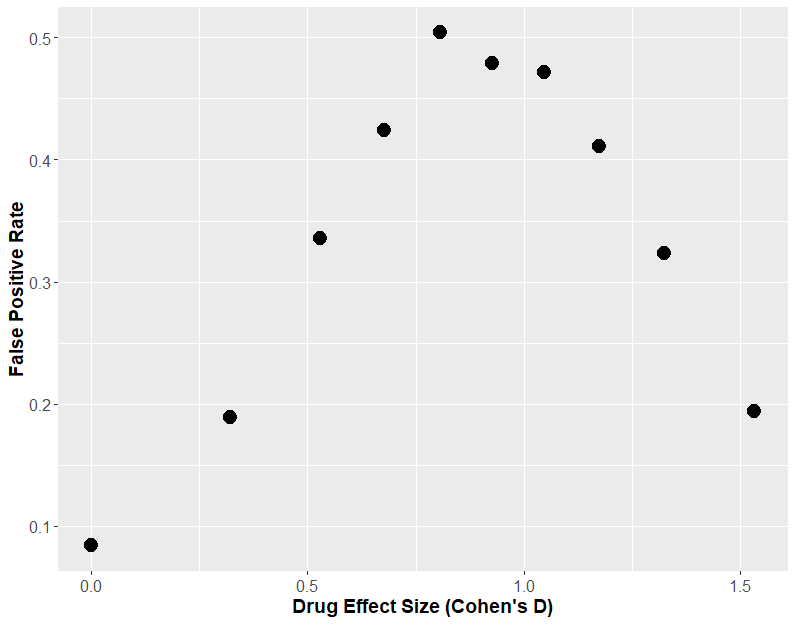
If we plot that same graph, but instead of using the effect size, we plot the theoretical power of the statistical test (i.e. how often the each t-test would find an effect of drug), we will understand why this “two t-test” approach is so fraught.
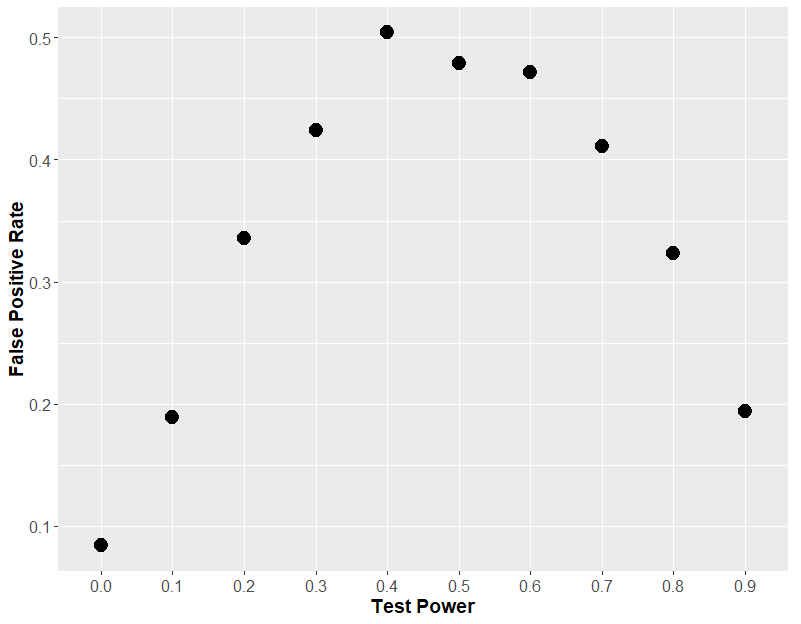
You see, it comes down to statistical power. If each t-test has very low power, then both t-tests will always be insignificant, so you will never see an effect of sex. If each t-test has a very high power, then both t-tests will always be significant, and so again, you will never see an effect of sex. But in the middle, when the t-test has about 50% power, then 50% of t-tests will be significant, which means that on average, in 50% of the cases, one test will be positive and one will be negative, leading you to erroneously conclude that sex has an effect.
So what should you do instead? You should run a 2-way ANOVA. A 2-way ANOVA allows you to investigate if there is an effect of drug, if there is an effect of sex and importantly, if there is an interaction of these two factors, i.e. that the effect of drug depends on sex. If we do that, our problems go away.
But maybe you think “Well maybe this using a 2-way ANOVA stops us making false positives, but it ruins out ability to detect if sex has an effect at all? Not really. If we change the effect size of drug, and the effect size of sex, and see how often the test can detect if sex has an effect of drug, we get some very curious results.
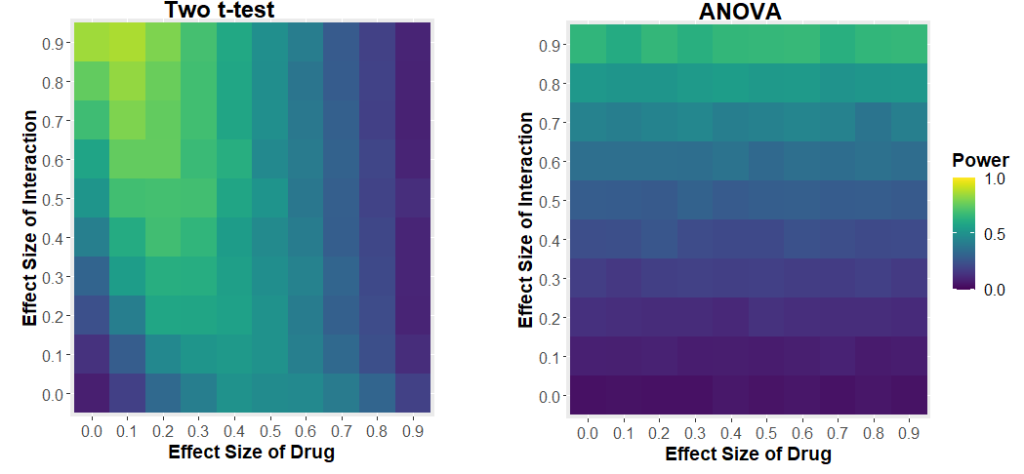
We see that the power of the two t-test approach to detect the interaction depends on the effect size of the drug. If the drug has a large effect, it drowns out the effect of the interaction. The two-way ANOVA approach has much more sensible behaviour: your ability to detect the interaction only depends on the size of the interaction.
Hopefully you understand that this is not specific to the effect of drugs and sex. If you perform 2 t-tests looking at some intervention in two different situations, and one is significant, and one isn’t, you cannot conclude that the intervention has a different effect in those two situations. You need to perform some test that actually compares the effect of the intervention in the two cases, most notably, a two way ANOVA.
Finally, I want to say that I am not the first one to point this out. There have been warnings published about this before, like in “The Difference Between “Significant” and “Not Significant” is not Itself Statistically Significant” By Gelman and Stern, and “Erroneous analyses of interactions in neuroscience” by Nieuwenhuis et al.
]]>However, when you ask how PCA works, you either get a simple graphical explanation, or long webpages that boil down to the statement “The PCAs of your data are the eigenvectors of your data’s covariance matrix”. If you understood what that meant, you wouldn’t be looking up how PCA works! I want to try to provide a gateway between the graphical intuition and that statement about covariance and eigenvectors. Hopefully this will give you 1) a deeper understanding of linear algebra, 2) a nice intuition about what the covariance matrix is, and of course, 3) help you understand how PCA works.

The Very Basics
So why do we use PCA and what does it do? (If you’re already familiar with why you’d use a PCA, skip to inside the PCA). Lets say we’re on a project collecting some images of the cells from breast growths, growths which are either benign or cancerous. We’ve just started collecting data, and from each of the images, we’ve calculated a bunch of properties, how big the cells are, how round they are, how bumpy they look, how big their surface area etc etc etc, lets say we measure 30 things. Or put another way, our data has 30 dimensions. We’re worried there is no difference in any of the parameters between the benign and cancerous cells. So we want to have a look. But how do you plot 30 dimensional data? You could compare each dimension 1 by 1, e.g. how smooth are cancerous cells vs the benign cells, how big are the cancerous cells vs the benign cells. And that might be plausible for 30 dimensional data. But what if you data had 1000 dimensions? Or 10,000 dimensions? Here comes PCA to save the day. It will squish those 30 or 10,000 dimensions down to 2, i.e previously, every cell had 30 numbers associated with it: its bigness, its roundness etc. Now it just has 2 numbers associated with it. We can plot those two numbers on a good old fashion scatter plot, and it allows us to see if there is some difference between the malignant and benign cells.
We can find data just like the one I mentioned thanks to the Breast Cancer Wisconsin dataset. We can perform PCA on it and we can plot the result. In this case we see that it looks like there is some difference between the cancerous and benign cells
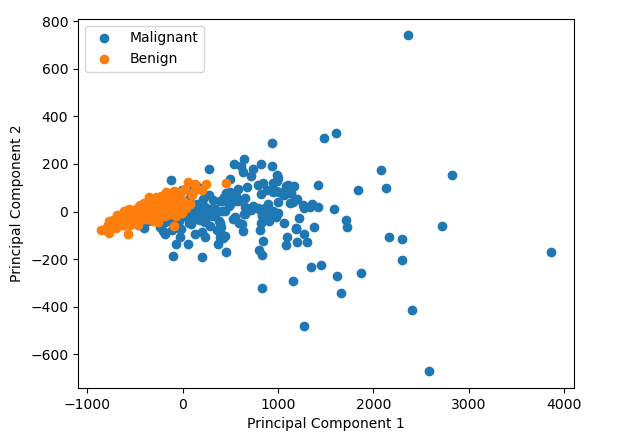
But what did we just do? How do the the two numbers (labelled Principal Component 1 and Principal Component 2 in the graph above) relate to the original data points in the data? It’s very hard to picture what’s going on in 30 dimension data, but if we reduce it down to 2D data, what is doing on becomes pretty intuitive.
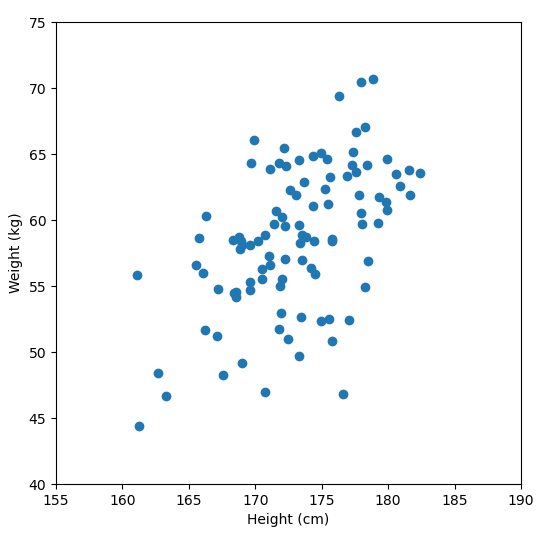
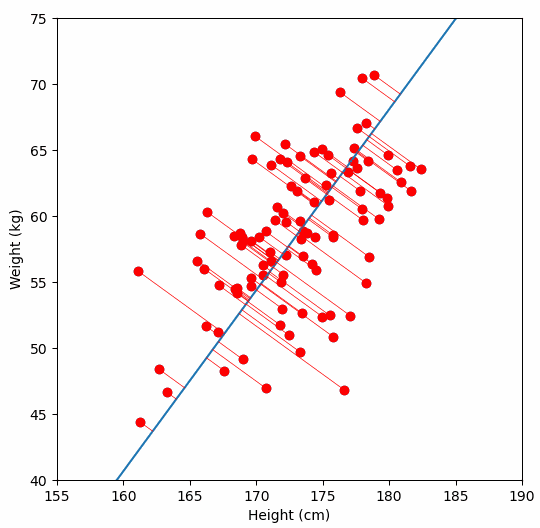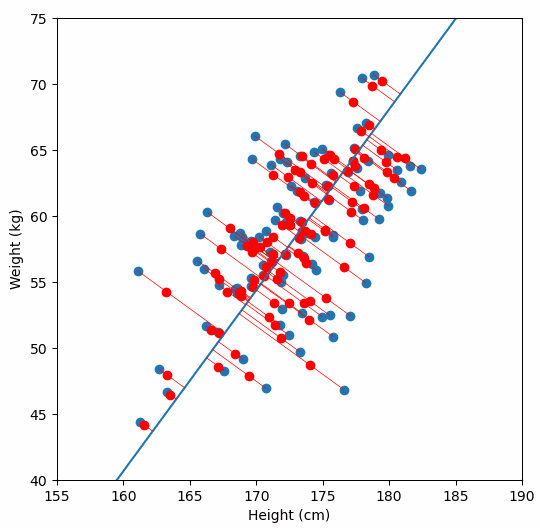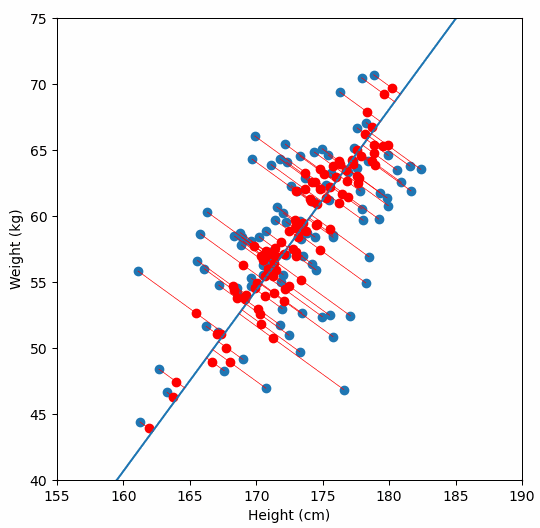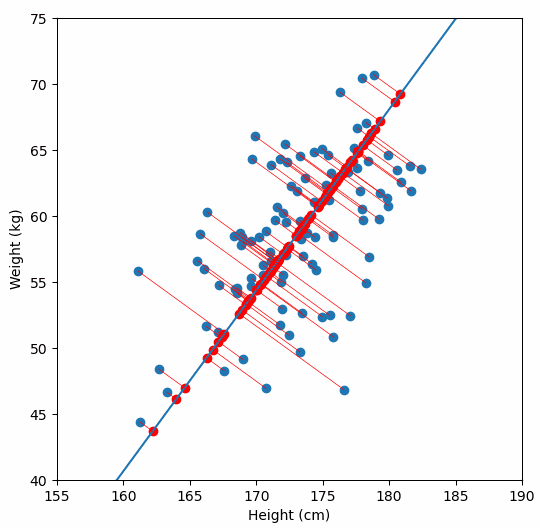
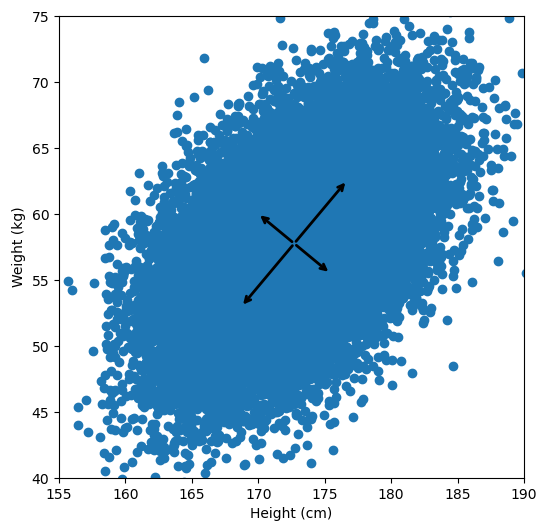
Let’s say we have some data of 50 people’s height and weight.
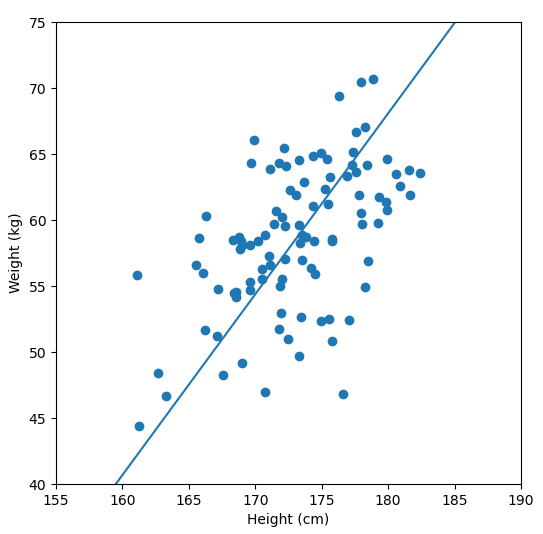
In order to perform a PCA, we first find the axis of greatest variation, which is basically the line of best fit. This line is called the first principal component.
Finally, we “project” our data points onto first principal component. Which means, imagine the line of best fit is a ruler. Each data points new value is how far along the ruler it is.
Previously, each individual was represented by their height and weight, i.e. 2 numbers. But now, each individual is represented by just 1 number: how far along the blue line they are. Because our original data has 2 dimensions, there is also a second principal component, which is perpendicular (or “orthogonal”) to the first principal component. In higher dimensions, things get difficult the visualize, but in practice the idea is the same: we get a bunch of principal components, with the first one being the line through our data in the direction of most of the variance, and each subsequent line being orthogonal to the previous, but in the direction of the next most variance. We can then project our data onto as many or as few of the components as we wish.
Inside the PCA
But what does that have to do with this opaque statement that “PCA is the eigenvectors of the covariance matrix”? First we need to understand what a covariance matrix is.
The Covariance Matrix
If you’re familiar with Pearson’s R, i.e. the correlation coefficient, then you basically understand what covariance is. To calculate the covariance between two sets of measurements x and y, you calculate:
If you don’t speak math, this simply says: subtract the mean of x from all of your data points in x, then subtract the mean of y from all the data points in y. Take the resulting two lists of numbers, and multiply each value in x, by its corresponding element in y. Finally, take the average of those products. What this means is that if the covariance is large and positive, then x goes above the mean while y goes above the mean. If the covariance is large and negative, then x goes up while y goes down (or vice versa). If before you calculate the covariance, you z-score/normalize your data (i.e. subtract the mean, and divide by the standard deviation), then when you calculate the covariance, you are calculating Pearson’s R.
The covariance matrix is just an organized way of laying out the covariance between several measurements. For instance, if you had three measurements, A, B and C, then the covariance matrix would be a 3×3 matrix, with the covariance between the measurements laid out like this:
Notice, down the diagonal of the matrix is cov(A,A), cov(B,B) and cov(C,C), the covariance of each measurement with itself. It turns out this is exactly equal to the variance of A, B and C. Again, if you normalized your data before calculating the covariance matrix, then the diagonal of the matrix would be filled with 1s, and all the other elements would be the Pearson’s R of each pair of measurements.
Linear Transformations and Eigenvectors
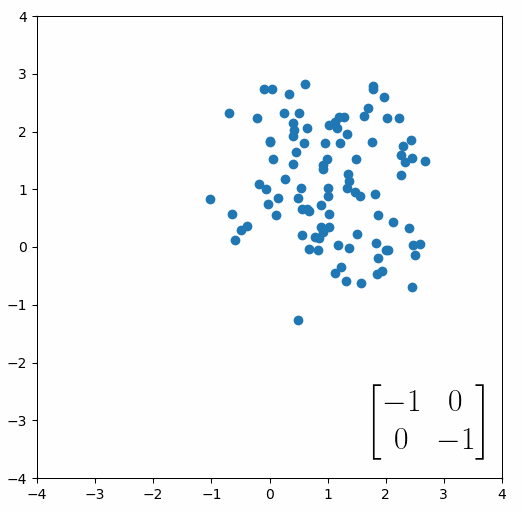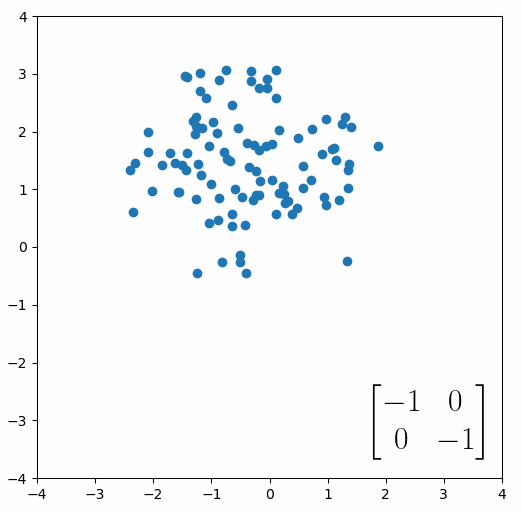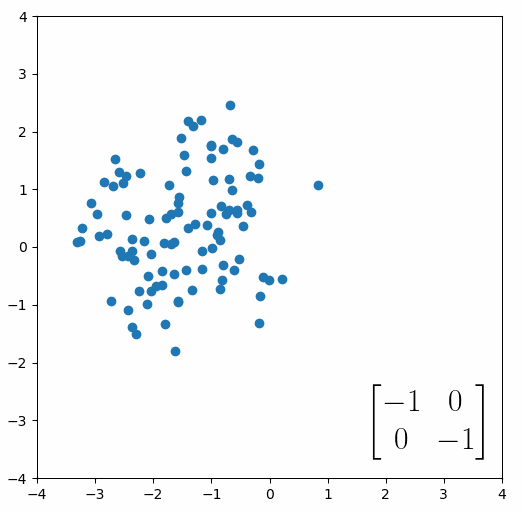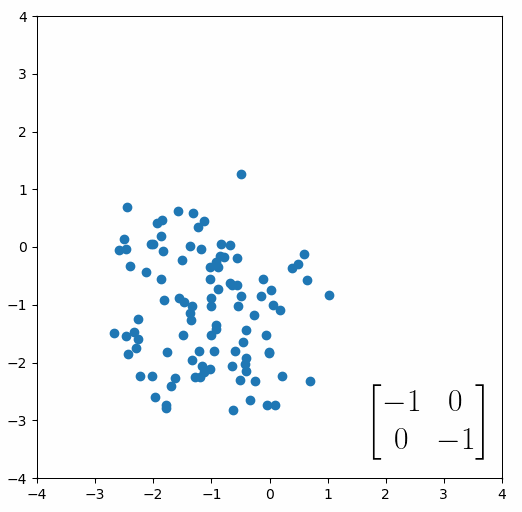
The next thing we need to understand is that basically any matrix can represent a “linear transformation”, which essentially means, a matrix contains a set of rules for moving data points around. A matrix “moves” data points whenever you multiply those data points by the matrix. Below we see a cloud of data points being rotated around the point (0,0) by multiplying the points values by the matrix [-1 0; 0 -1].
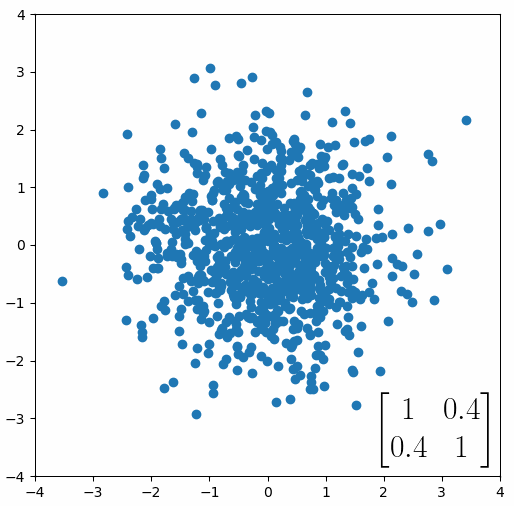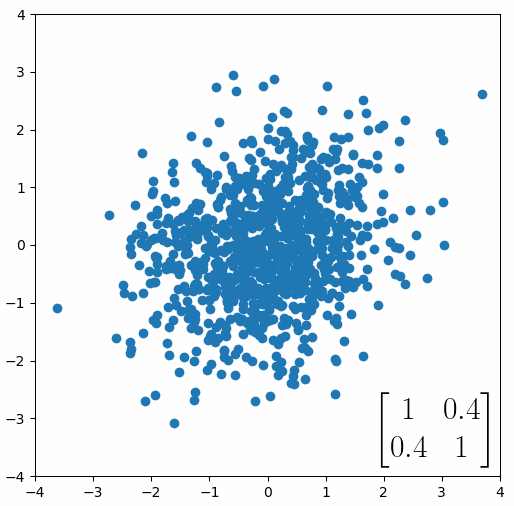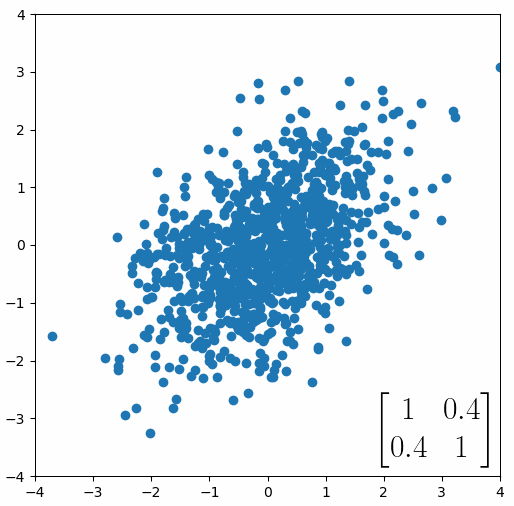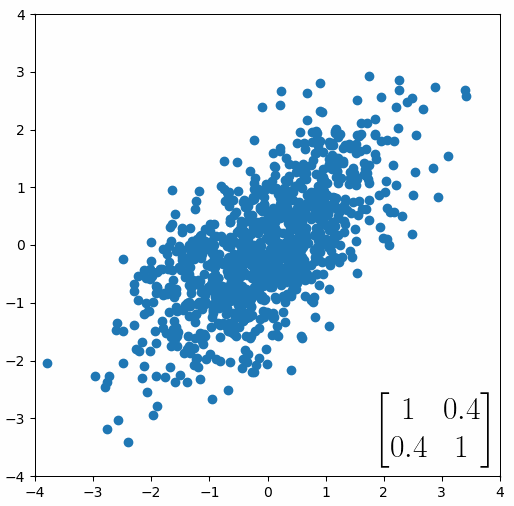
The linear transformation that I really want to focus on, is “shearing”. In the figure below, data points are sheared by multiplying them by the matrix [1 0.4; 0.4 1].
Looking at this animation, I want you to notice something: if a data point had started at the point (1,1) it would have ended up at some other point (z,z), i.e. it would have stayed on the line y = x. This is of course also true for points (2,2), (3,3) or (42,42). All the points that started on the line y = x would have ended up on the line y = x. And so, that line is an eigenvector of our matrix. Perhaps an animation would be helpful:
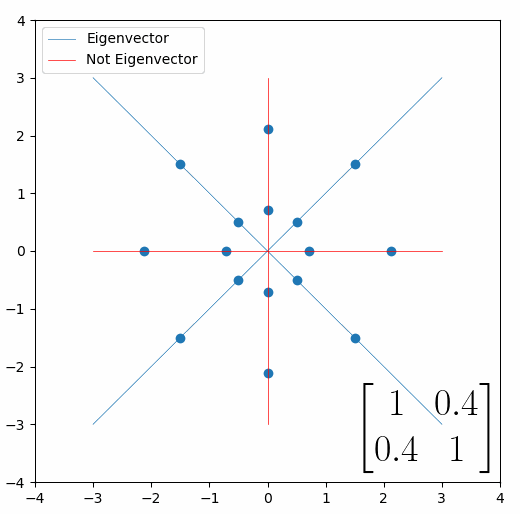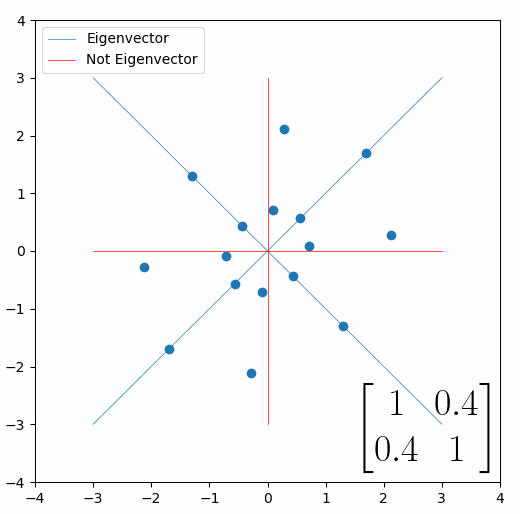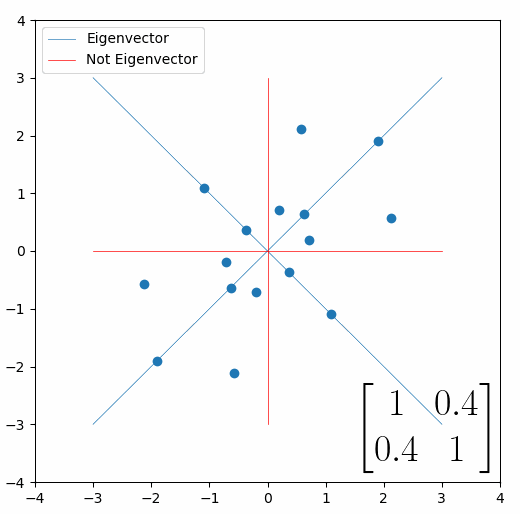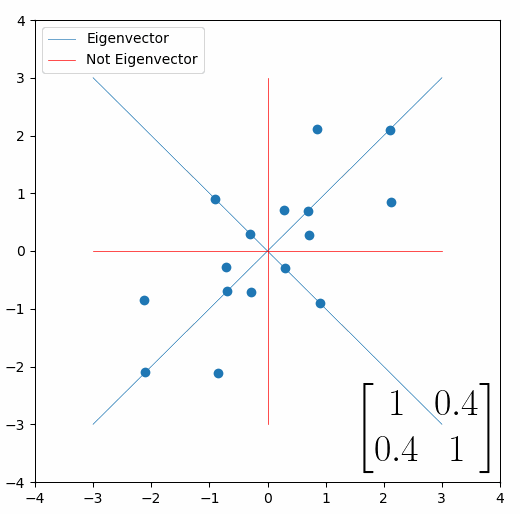
The eigenvalue is how far long this line a data point would move. So, if a point started at (1,1) and ended at point (2,2), then the transformation would have a eigenvalue of 2. If a data point started at (4,4) and ended at (2,2), the transformation would have a eigenvalue of 0.5. So eigenvectors/values are just a simplified way of looking at a matrix/linear transformation, kind of like how we can describe a journey with a step by step itinerary, (the matrix) or by simply the direction we’re heading (the eigenvector) and how far we’re going (the eigenvalue). So, the eigenvectors of a linear transformation are lines that, if a data points starts on it, then after the linear transformation the data point will still be on it. Or even more simply, the eigenvectors of a matrix are the “directions” of the linear transformation/matrix. The linear transformation represented by the matrix [1 0.4; 0.4 1] has two eigenvectors, one on the line y = x, but another on the line y = -x. On the first eigenvector, data points expand away from the center of the graph, so its eigenvalue is 1.4, but on the other line they contract towards the center, so its eigenvalue is 0.6.
Covariance and the Eigenvector
Here comes the magic bit: we can think of the covariance matrix as a linear transformation. Let’s say we had some data that had some correlations within it, and we calculated its covariance matrix, T. If we generated some random normally distributed data, and we multiply it by √T, then it would transform that data so that it had the same standard deviations and correlations we see within our data. So a covariance matrix contains the information to transform random, normally distributed data, into our data. Or put a mathematically:
We remember that the eigenvectors of a linear transformation are essentially the directions in which our linear transformation is smearing the data. So the eigenvectors and values of √T will tell us in what directions our data is been smeared in and by how much. Well it turns out that the eigenvectors of T are exactly equal to the eigenvectors of √T, and the eigenvalues of T are just the squares of the eigenvectors of √T. So, we can just calculate the eigenvectors/values of the covariance matrix without having the calculate √T. And this is how we perform PCA. We calculate the covariance matrix of our data, we calculate the eigenvectors of the covariance matrix, and this gives us our principal components. The eigenvector with the largest eigenvalue is the first principal component, and the eigenvector with the smallest eigenvalue is the last principal component.
I know that’s a lot to take in, so lets do some code and make some graphs to see this idea in action.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.decomposition import PCA
from scipy.linalg import sqrtm
#Load the data
df=pd.read_csv('http://www.billconnelly.net/data/height_weight.csv', sep=',',header=None)
df = np.array(df)
#Plot the data
fig = plt.figure(figsize=(6,6))
plt.scatter(df[:,0], df[:,1])
ax = plt.gca()
#Perform the PCA
pca = PCA(n_components=2)
pcafit = pca.fit(df)
#Display the components
for comp, ex in zip(pcafit.components_, pcafit.explained_variance_):
rotation_matrix = np.array([[-1, 0],[0, -1]])
ax.annotate('', pcafit.mean_ + np.sqrt(ex)*comp, pcafit.mean_, arrowprops={'arrowstyle':'->', 'linewidth':2})
ax.annotate('', pcafit.mean_ + rotation_matrix@(np.sqrt(ex)*comp), pcafit.mean_, arrowprops={'arrowstyle':'->', 'linewidth':2})
plt.xlabel("Height (cm)")
plt.ylabel("Weight (kg)")
plt.xlim((155,190))
plt.ylim((40,75))
plt.show()
For references sake, the first principal component is (-0.64, -0.77) and the second is (0.77, -0.64). Now let’s calculate them with the way I laid out: by taking the eigenvectors of the covariance matrix:
#Calculate the covariance matrix of the data
T = np.cov(df.T)
#Calculate the eigenvectors and eigenvalues
eigvals, eigvects = np.linalg.eig(T)
for e_val, e_vec in zip(eigvals, eigvects.T):
print("Eigenvector = {0}, eigenvalue = {1}".format(e_vec, e_val))
Eigenvector = [-0.76873112 0.6395721 ], eigenvalue = 12.620620110675544 Eigenvector = [-0.6395721 -0.76873112], eigenvalue = 38.80431240231845
So the eigenvector with the largest eigenvalue is the first principal component, and it’s calculated as (-0.64, -0.77). Exactly the same as the above version. However, the second principal component is calculated as (-0.77, 0.64), while above it was calculated as (0.77, -0.64). What’s going on? Note, my component points to the top left, while the version above points to the bottom right. But these two components fall on the same line. So while these components are not numerically identical, they are functionally identical. This difference is due to the fact that sklearn uses a computational shortcut to calculate the principal components.
But now lets see the second trick, can we use the covariance matrix to transform random data to look like our original data?
#Calculate the covariance matrix of the data.
#Because numpy.cov works row-wise, we have to
#use the matrix transpose, i.e. the columns
#become rows.
T = np.cov(df.T)
sqrtT = sqrtm(T)
#Generate some normally distributed random data
#and organize it into a matrix.
sample_size = 10000
x = np.random.normal(0, 1, sample_size)
y = np.random.normal(0, 1, sample_size)
A = np.vstack((x,y))
#Perform linear transformation
#The @ symbol does matrix multiplication
Atransformed = sqrtT @ A
#Print results
print("The covariance matrix of the original data is:")
print(T)
print("The covariance matrix of our random data before transformation is:")
print(np.cov(A))
print("The covariance matrix of our random data after transformation is:")
print(np.cov(Atransformed))
Which results in:
The covariance matrix of the original data is: [[23.33112407 12.87344728] [12.87344728 28.09380845]] The covariance matrix of our random data before transformation is: [[1.02388073 0.00596005] [0.00596005 0.99430078]] The covariance matrix of our random data after transformation is: [[23.90996341 13.13354086] [13.13354086 28.06547344]]
Or graphically, we can show how multiplying random gaussian data points by the square root of some data’s covariance matrix, turns that gaussian data into our data:
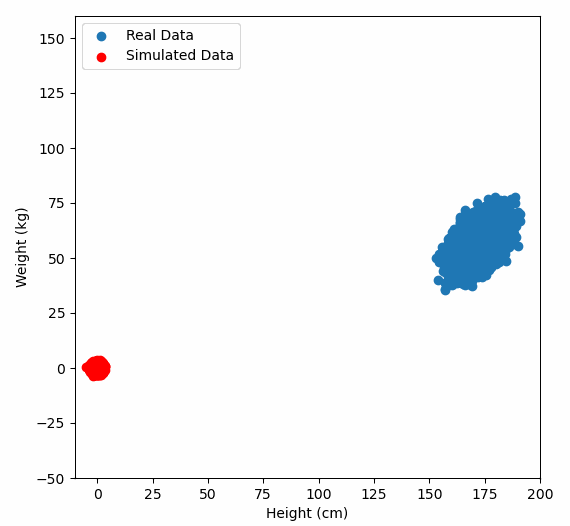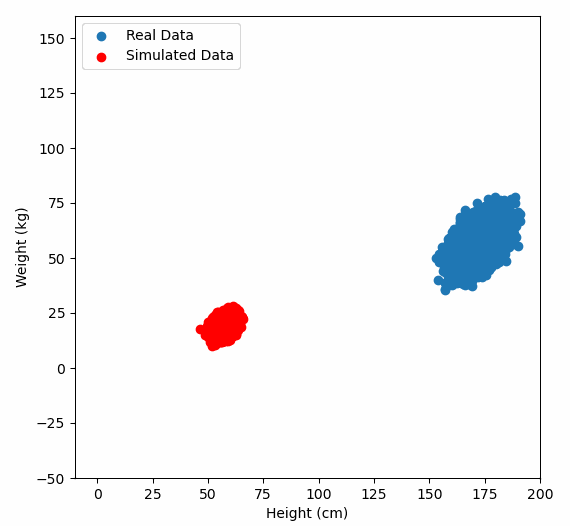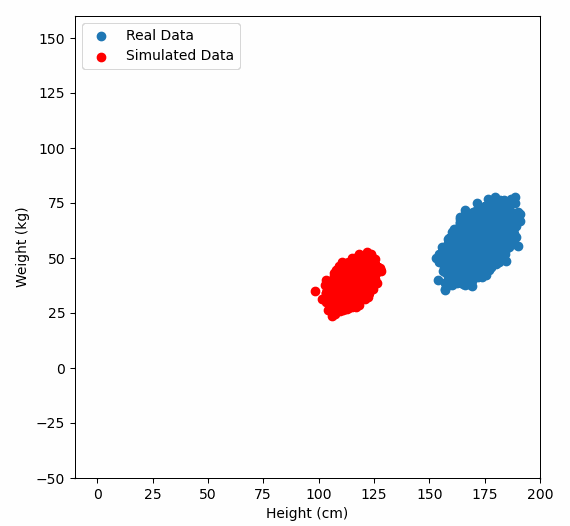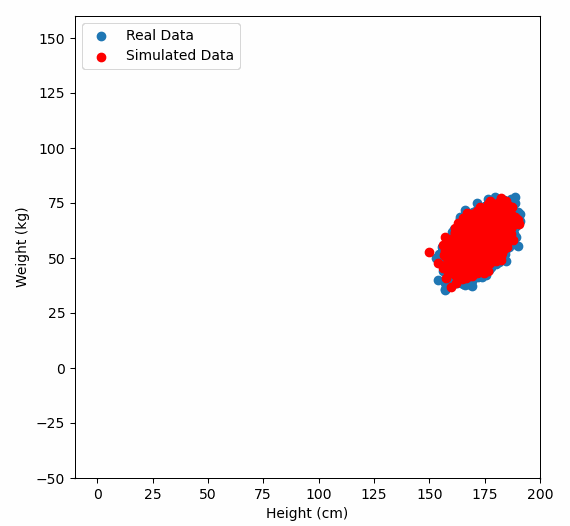
So what are the take away points?
- Principal Component Analysis (PCA) finds a way to reduce the dimensions of your data by projecting it onto lines drawn through your data, starting with the line that goes through the data in the direction of the greatest variance. This is calculated by looking at the eigenvectors of the covariance matrix.
- The covariance matrix of your data is just a way of organizing the covariance of every variable in your data, with every other.
- A matrix can represent a linear transformation, which means if you multiply some data points by the matrix, they get moved around the graph.
- The eigenvectors of a linear transformation are the lines where if a data point started on that line, they end on that line, and the eigenvalue says how far they have moved. We can think about eigenvectors being kind of like the direction of a linear transformation.
- A covariance matrix can be used as a linear transformation, and the square root of the covariance matrix of some data will perform a linear transformation that moves gaussian data points into the shape of our data, i.e. they will have the same standard deviations and correlations as our data.
- So, the eigenvectors of the square root of the covariance matrix tells us in what direction our data has been smeared away from perfectly normally distributed and the eigenvalues tell us how far. It turns out, that the eigenvalues of the square roof of the covariance matrix are exactly equal to the eigenvalues of of the covariance matrix, so we just work with the covariance matrix. This direction of the smearing is the same this as the principal components, and how far our data was smeared tells us which direction has the greatest variance. The eigenvector with the largest eigenvalue is the first principal component, the eigenvector with the second largest eigenvalue is the second principal component, etc etc etc…
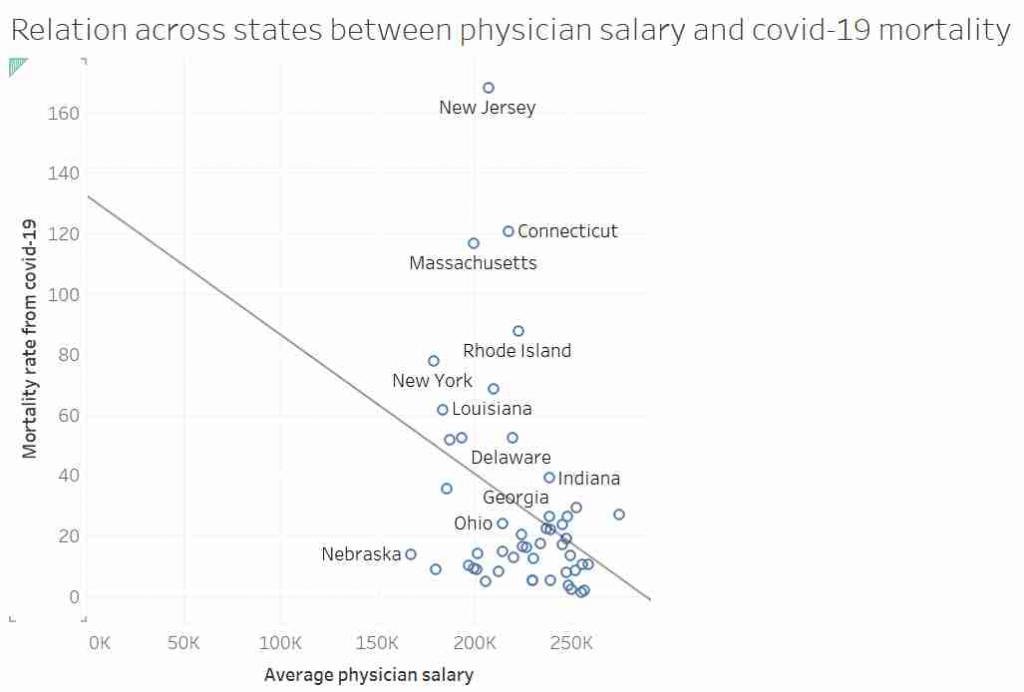
I’d like to talk about this graph, data, regression, causation and data analysis.
Before I get started I want to point out that I am not an epidemiologist or an expert in virology or public health. This post is not meant to be guidance on policy. I am using an unusual graph to illustrate problems in data analysis. That said, I also suspect there is a lot of truth in the final conclusion.
Part 1: Things are not always what they seem.
This graph, it was suggested, showed that in US states where doctors are paid more have lower mortality rates from COVID-19. After all look at the trend line!
Most “sensible” people, myself included, saw no relationship between these two measures. And needless to say, the replies to the tweet did not shy away from pointing that out. Thankfully, in a rare moment of wisdom, instead of joining the pile-on, I simply shared the image with my friend and collaborator, Dr Jack Auty. He did the sensible thing and extracted the data using WebPlotDigitizer and run the data through R. I’ve put my data extraction up online, so you can follow along
dat <- read.csv("http://www.billconnelly.net/uploads/covid1.csv")
mdl <- lm(dat$Mortality.Rate ~ dat$Salary)
summary(mdl)
Call:
lm(formula = dat$Mortality.Rate ~ dat$Salary)
Residuals:
Min 1Q Median 3Q Max
-39.860 -17.289 -8.606 7.373 131.549
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 125.7330 41.7867 3.009 0.0042 **
dat$Salary -0.4352 0.1854 -2.347 0.0232 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 32.81 on 47 degrees of freedom
Multiple R-squared: 0.1049, Adjusted R-squared: 0.08584
F-statistic: 5.507 on 1 and 47 DF, p-value: 0.0232So, I have run a linear regression of salary against mortality, and the summary() function returns all the stuff you typically need to know. And what do we see: well the dat$Salary coefficient is statistically significantly different from zero, meaning the line of best fit is not horizontal. Furthermore it’s negative, meaning that the line of best fit suggests that in states where doctors are paid more, the COVID mortality rate is lower. Finally, the R-squared is around 0.1, meaning that about 10% of the variance in mortality can be explained by the changes in doctors salaries. So does that means the original tweeter was correct?
Well hang on. We’ve run a linear regression, what are the assumptions of linear regression? That is to say, what conditions must we meet in order for the numbers that come out of the linear regression to mean what we think the mean. They are:
- Linearity – In this case, that the relationship between salary and mortality rate is a line.
- Independence – Typically, this is explained by saying that each observation must not be affected by any of the other observations.
- Homoscedasticity – That that variance of Y doesn’t vary as you move along X. For instance, if we wanted to do a regression of height against weight for all the species in the animal kingdom we would be in trouble as the variances of small animals is certainly going to be less than the variance of large animals. Percentage-wise it might be the same, but in units of length, the variance of ants is going to be less than elephants.
- Normality – That the residuals of fit, (that is the distance between the data and the line of best fit) are normally distributed. This is often misinterpreted as that the data itself needs to be normally distributed. But no, it is just the residuals. Though, if this data set was somehow much bigger, and we had thousands of states, if were were able to select a dozen states that almost the same doctor’s salary, we would expect the mortality rate of those dozen states to be normally distributed.
It is the last two assumptions that are often violated, especially when the data goes across more than an order of magnitude. So can we test if this data obeys the assumptions? Yes, we can. We simply say:
plot(mdl)This generates 4 graphs, two of which I want to focus on. The first one shows the residuals against the fitted value
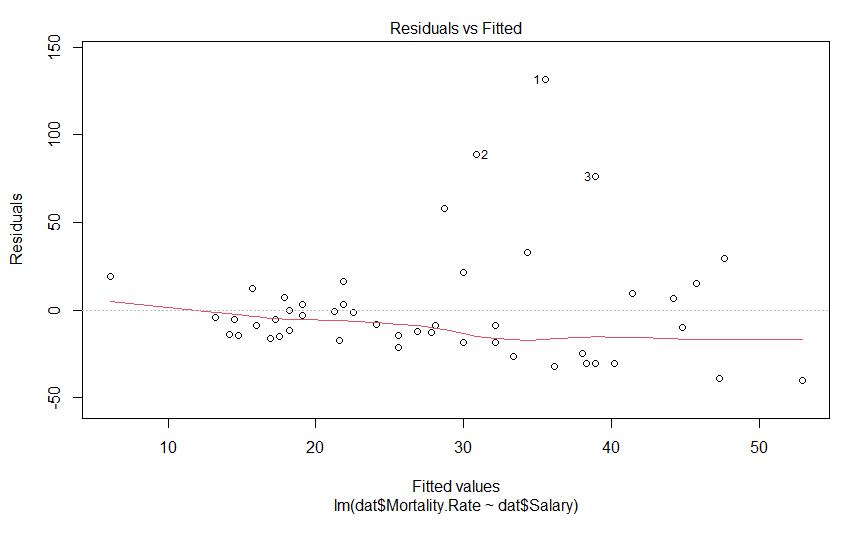
We don’t see anything that terrible, but it’s not perfect either. We would hope to see these data points in nice cloud, where you could draw a horizontal line of best fit. This graph shows us how the data regarding assumptions 1, 3 and 4. If the residuals appear to follow a smooth curve, chances are you’ve broken the assumption of linearity. If the absolute value of the residuals get larger as the fitted values get larger, you’d broken the assumption of homoscedasticity Finally, if the residuals don’t look evenly spread above and below the horizontal line, chances are, you’ve broken the assumption of normality. To my eyes, the data above the line is on average further away from the horizontal line than the data below it, and so I suspect the residuals aren’t normally distributed. Thankfully, the next graph will give us a much clearer answer
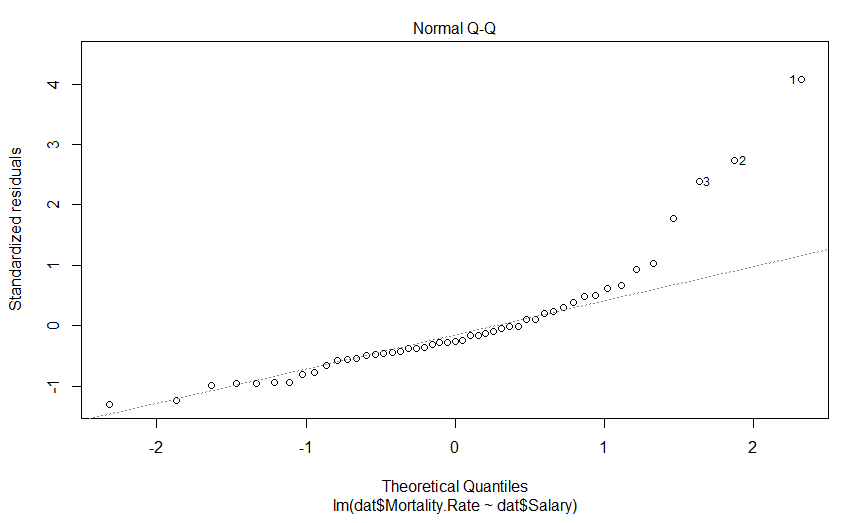
This is a quantile-quantile (Q-Q) plot of our residuals (transformed into a Z-score) against where you would expect them to fall if they were normally distributed. The point here is that if our residuals were normally distributed, they should fall on this dashed line, which they clearly do not, and importantly, they appear to deviate in a predictable fashion.
I suspect that if we log transform our mortality data, our data will be much more nicely behaved. Indeed, log-transforming data typically is necessary when it varies by more than an order of magnitude. So lets do that, and see what our graphs look like
mdl.log <- lm(log(dat$Mortality.Rate) ~ dat$Salary)
plot(mdl.log)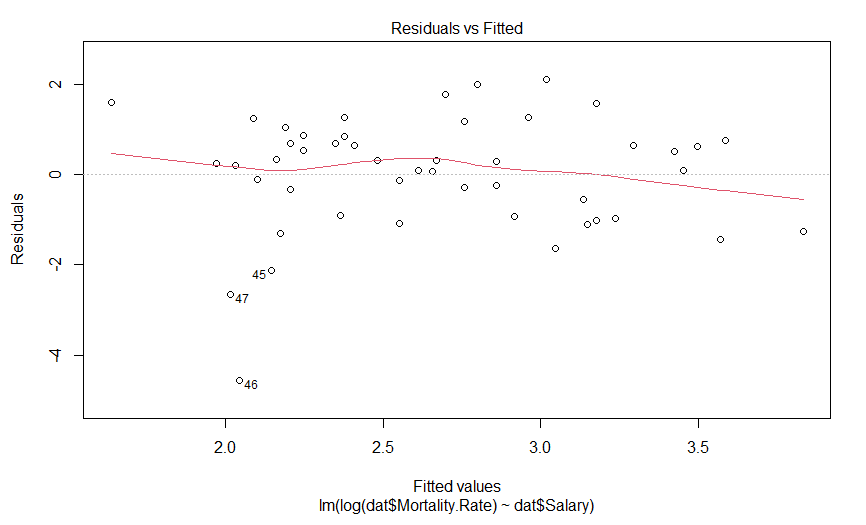
Our plot of residuals against fitted values looks like a bit of an improvement, but it wasn’t that much of an abomination to begin with. But what about the Q-Q plot?
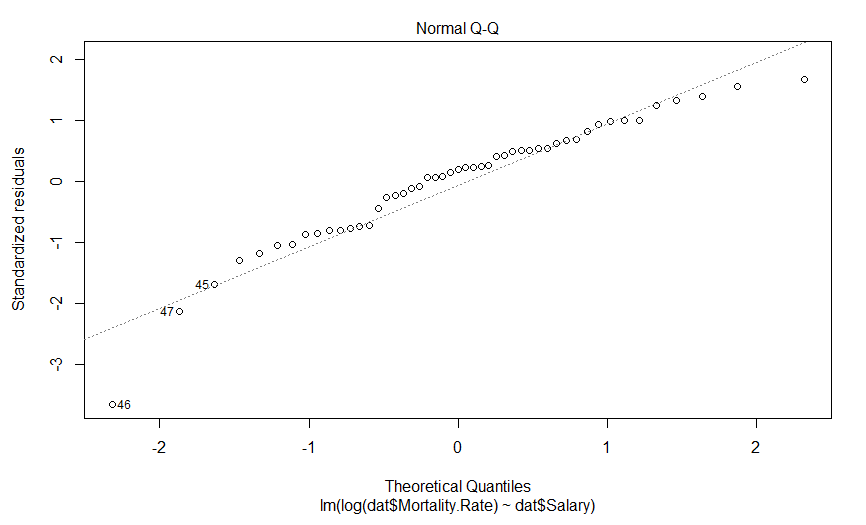
Well this is certainly an improvement. It looks like there is still a predictably deviation from normality, but it isn’t anywhere near as aggressive and it only involves maybe three data points (as opposed to six).
So what does our regression actually say now
summary(mdl.log)
Call:
lm(formula = log(dat$Mortality.Rate) ~ dat$Salary)
Residuals:
Min 1Q Median 3Q Max
-4.5550 -0.9394 0.2459 0.7568 2.1001
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.250797 1.629428 4.450 5.25e-05 ***
dat$Salary -0.020417 0.007231 -2.824 0.00694 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.279 on 47 degrees of freedom
Multiple R-squared: 0.145, Adjusted R-squared: 0.1268
F-statistic: 7.973 on 1 and 47 DF, p-value: 0.006942So we have a very significant slope coefficient, which is still negative, and our R-squared value has gone up a bit. And what do our fits look like?
par(mfrow=c(1,2))
plot(dat$Salary, log(dat$Mortality.Rate))
abline(mdl.log)
par(mfrow=c(1,2))
plot(dat$Salary, dat$Mortality.Rate)
abline(mdl)
plot(dat$Salary, log(dat$Mortality.Rate))
abline(mdl.log)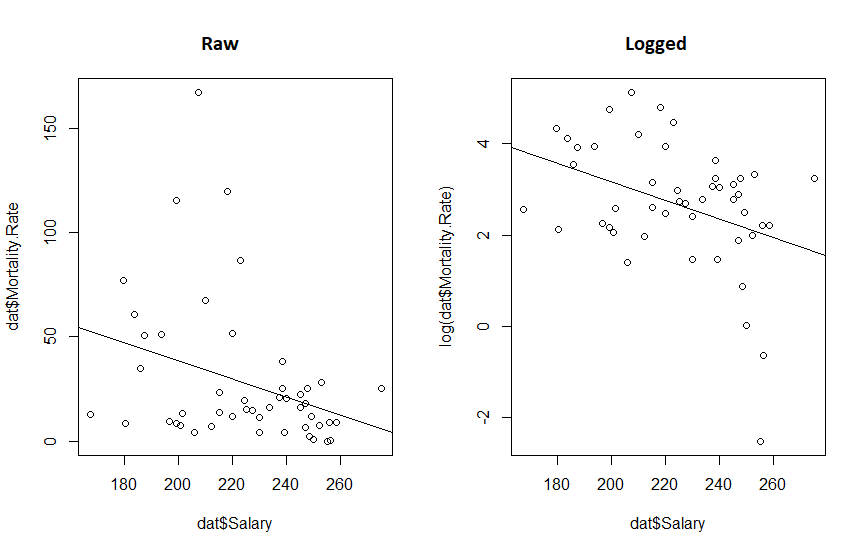
What we really see from this is that if the original twitter post had been displayed with appropriate axis, the whole fit would look a lot more convincing. We also see that transforming the data reduced the P value 10 fold and increased our R-squared. So the take away message here is:
it’s a good idea to make your graphs so they show your point, and but it’s a great idea to think about your data before you subject it to statistical methods.
Part 2: The wise know their limitations; the foolish do not.
Despite the statistical relationship between these two sets of data, what should we take away from this? Does anyone expect that if we started paying doctors more today, that the mortality rate of COVID would drop in the next few weeks? I hope not. Perhaps though, states which pay doctors more have attracted better doctors who have, in turn, improved the health care sector in those states? Or perhaps doctors are paid more in states that value well being more, and those states also contain more people that wear masks? These seems like reasonable hypotheses. Here, the word hypothesis is important. Because the regressions we were performing are hypothesis tests. And every time we perform a hypothesis test, there is a chance that we will incorrectly support our hypothesis, or incorrectly reject it. And this is why we cannot just go around randomly investigating every possible pair of data we can think of, as eventually we will always find two variables that are related, but that doesn’t mean the relationships are causative, or even important, after all correlation does not imply causation. To put it simply, this apparent significant relationship may be nothing more than coincidence.
On the other hand, calling the result a coincidence may be being foolish as well. Another possibility is that states which pay doctor’s more are more wealthy, educated or sparsely populated, and is it those variables that are causative in effecting mortality rates. So the relationship we observed was real, but not causative. That is to say there is a variable that is co-linear with doctor’s salary that we have not observed, and this variable causally relates to mortality rates, otherwise known as the omitted variable bias.
While a full analysis that attempts to control for these various variables may be warranted, the real point I want to get at is that no matter what kind of regression we do, establishing the true cause of why some states show much lower mortality rates will always be difficult without an (quasi) experimental approach. Using an evidence based hypothesis will always boost the validity of a finding, but there is always a chance of the omitted variable bias. Or more simply, when performing regression on retrospective data, no matter how carefully it is performed, or how sensible the hypothesis is, it can never establish causation.
Part 3: Garbage in, Garbage out.
There was something missing from the first post, something I should have noticed the absence of: the data source. Where did the data come from? And what does it mean by mortality rate? Is that per patient with COVID, or across the whole population?
So I went and got the best data I could find, I used the US Bureau of Labor Statistics for the salary information, and the CDC for the mortality rate (total deaths from COVID per 100,000). Because I was convinced this would be important, I got the GDP per capita from the Bureau of Economic Analysis. Finally, I had a strong feeling that wealth inequality would also be important, I included each states Gini coefficient taken from data from the US Census Bureau. Vermont was excluded as the Bureau of Labor Statistics didn’t have their data for physician salary. The data is available here.
I ran a simple model
mdl <- lm(log(mort.rate) ~ salary + gdp + gini, data = cov.dat)
summary(mdl)
Call:
lm(formula = log(mort.rate) ~ salary + gdp + gini, data = cov.dat)
Residuals:
Min 1Q Median 3Q Max
-2.08874 -0.61624 0.01062 0.68168 1.77905
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.262e+00 4.056e+00 -1.544 0.129
salary -5.532e-06 6.502e-06 -0.851 0.399
gdp 7.384e-06 6.410e-06 1.152 0.255
gini 2.097e+01 7.111e+00 2.949 0.005 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9405 on 46 degrees of freedom
Multiple R-squared: 0.3398, Adjusted R-squared: 0.2968
F-statistic: 7.893 on 3 and 46 DF, p-value: 0.0002369We see that salary and GDP have no effect on mortality, but the Gini coefficient does: as the Gini coefficient goes up (wealth gets more unequal) the mortality rate rises. However, while coliniarity between a variable you include and one you exclude can lead to omitted variable bias mentioned above, colinarity is a problem when you include two variables that are colinear too. It leads to poor estimates of coefficients, and in fact, can even make them point in the wrong direction.
In order to test for colinarity, we can import the mctest library and apply all the tests, the most important one being the Farrar – Glauber Test, which tells us some coliniarity exists.
library(mctest)
omcdiag(mdl)
Call:
omcdiag(mod = mdl)
Overall Multicollinearity Diagnostics
MC Results detection
Determinant |X'X|: 0.6306 0
Farrar Chi-Square: 21.7442 1
Red Indicator: 0.3721 0
Sum of Lambda Inverse: 4.0983 0
Theil's Method: 0.0965 0
Condition Number: 78.0226 1
1 --> COLLINEARITY is detected by the test
0 --> COLLINEARITY is not detected by the testAnd when we investigate who is to blame, if we run linear regressions between the terms, we see that the relationship between doctor’s salary and Gini coefficient is significant.
summary(lm(salary ~ gini, data = cov.dat))
Call:
lm(formula = salary ~ gini, data = cov.dat)
Residuals:
Min 1Q Median 3Q Max
-42837 -12142 218 12401 37456
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 447392 59221 7.555 1.04e-09 ***
gini -508096 126813 -4.007 0.000213 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 20970 on 48 degrees of freedom
Multiple R-squared: 0.2506, Adjusted R-squared: 0.235
F-statistic: 16.05 on 1 and 48 DF, p-value: 0.0002135Though curiously it appears that states that pay their doctors more have a lower Gini coefficient.
When dealing with colinear data, there are a variety of approaches one can take, but the simplest is simply to simply remove the colinear variable with the least explanatory power, i.e. drop doctors salary. In doing so, we get another model, which suggests a very significant relationship between COVID mortality rates Gini coefficient, again, where states with unequal wealth distribution have high mortality rates. We also see that states with higher GDP per capita have higher mortality rates. Finally, we see an interaction, where states that have a high Gini coefficient and a high GDP. have a reduced morality rate.
> mdl <- lm(formula = log(mort.rate) ~ gdp * gini, data = cov.dat)
> summary(mdl)
Call:
lm(formula = log(mort.rate) ~ gdp * gini, data = cov.dat)
Residuals:
Min 1Q Median 3Q Max
-2.17381 -0.49555 0.06311 0.59163 1.39747
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.831e+01 7.967e+00 -3.554 0.000891 ***
gdp 2.781e-04 1.049e-04 2.652 0.010948 *
gini 6.232e+01 1.590e+01 3.919 0.000293 ***
gdp:gini -5.212e-04 2.012e-04 -2.591 0.012792 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.8855 on 46 degrees of freedom
Multiple R-squared: 0.4148, Adjusted R-squared: 0.3767
F-statistic: 10.87 on 3 and 46 DF, p-value: 1.618e-05But again, we should check for coliniarity
> omcdiag(mdl)
Call:
omcdiag(mod = mdl)
Overall Multicollinearity Diagnostics
MC Results detection
Determinant |X'X|: 0.0021 1
Farrar Chi-Square: 291.1233 1
Red Indicator: 0.6791 1
Sum of Lambda Inverse: 774.7488 1
Theil's Method: 2.0518 1
Condition Number: 221.7526 1
1 --> COLLINEARITY is detected by the test
0 --> COLLINEARITY is not detected by the testAnd every test tells us our data is colinear. Because there are only two variables in our model, we know GDP and Gini coefficients must be coliniar, and a linear regression shows us that as GDP per capita goes up, so does the Gini coefficient.
> summary(lm(gdp ~ gini, data = cov.dat))
Call:
lm(formula = gdp ~ gini, data = cov.dat)
Residuals:
Min 1Q Median 3Q Max
-29863 -12025 -1188 8563 110237
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -113477 60073 -1.889 0.06494 .
gini 375494 128636 2.919 0.00533 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 21270 on 48 degrees of freedom
Multiple R-squared: 0.1508, Adjusted R-squared: 0.1331
F-statistic: 8.521 on 1 and 48 DF, p-value: 0.005331So we are left with only one option, to run two models, one for the effect of the Gini coefficient, and one for the effect of GDP per capita, and we see exactly what the previous models told us, states with a higher GDP per capita or a more wealth inequality have high COVID mortality, but because we ran these models separately, we have no idea about how these variables interact.
> m1 <- lm(log(mort.rate) ~ gini, data = cov.dat)
> summary(m1)
Call:
lm(formula = log(mort.rate) ~ gini, data = cov.dat)
Residuals:
Min 1Q Median 3Q Max
-2.1904 -0.7170 -0.0506 0.7076 1.7694
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -9.574 2.652 -3.610 0.00073 ***
gini 26.551 5.680 4.675 2.42e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9394 on 48 degrees of freedom
Multiple R-squared: 0.3128, Adjusted R-squared: 0.2985
F-statistic: 21.85 on 1 and 48 DF, p-value: 2.418e-05
> m2 <- lm(log(mort.rate) ~ gdp, data = cov.dat)
> summary(m2)
Call:
lm(formula = log(mort.rate) ~ gdp, data = cov.dat)
Residuals:
Min 1Q Median 3Q Max
-2.72733 -0.58109 0.00395 0.72119 2.03738
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.793e+00 4.383e-01 4.090 0.000164 ***
gdp 1.649e-05 6.673e-06 2.471 0.017070 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.067 on 48 degrees of freedom
Multiple R-squared: 0.1129, Adjusted R-squared: 0.09438
F-statistic: 6.106 on 1 and 48 DF, p-value: 0.01707And what does out fits look like?
> plot(log(mort.rate) ~ gdp, data = cov.dat)
> abline(m2)
> plot(log(mort.rate) ~ gini, data = cov.dat)
> abline(m1)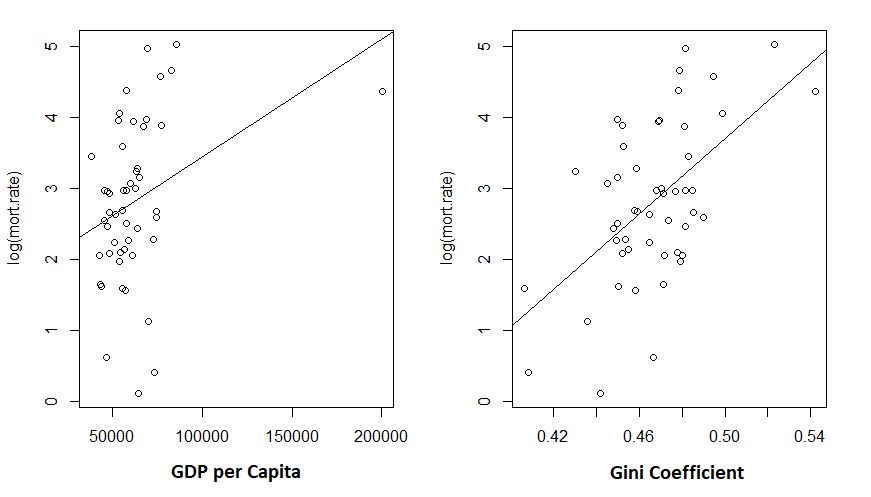
Given the low R-squared for the GDP fit, I’m not particularly shocked to see the unconvincing fit. But the Gini coefficient explained about 30% of the variance in mortality rates.
And do these two models appear to obey the assumptions of linear regression? Pretty much:
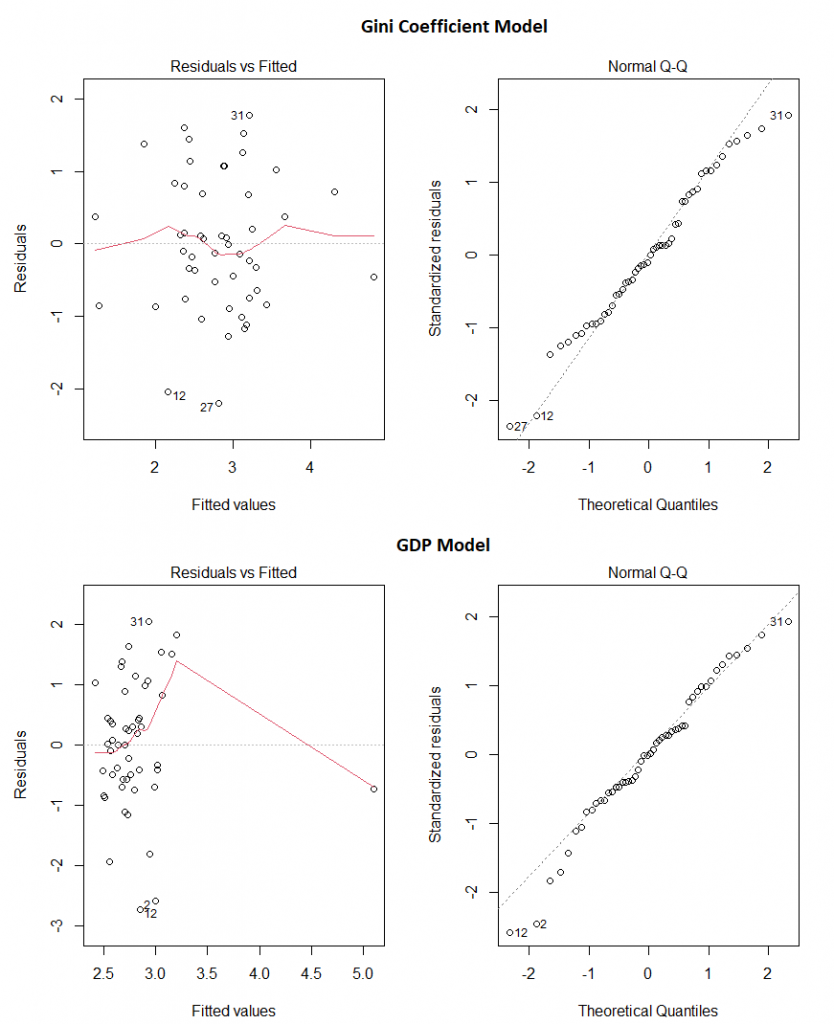
Our final take away message? Make sure the data you’re using comes from somewhere you trust, use your brain before you even start creating models, and then check the models assumptions before making any claims.
Overall…
So the original graph was a bad graph: it failed to tell the story it was intended to tell, simply due to the choice of range on the X axis. The analysis performed on it was bad because it failed to take into account even the simplest of covariates. Investigating the covariates opened a can of worms, and left me with data the strongly implicated wealth inequality in explaining why some states have much higher rates of mortality due to COVID than others. Though, of course, this analysis in no way can prove causation. As before, it could be some other causative variable that correlates with the Gini coefficient that is leading us to this conclusion.
]]>Near the start of any instructional manual on voltage clamp, there is a section describing how when you first break into a cell you correct for whole cell capacitance and series resistance, turning the capacitive transient you see in response to a voltage step into a smoothly rising curve (Fig 1).
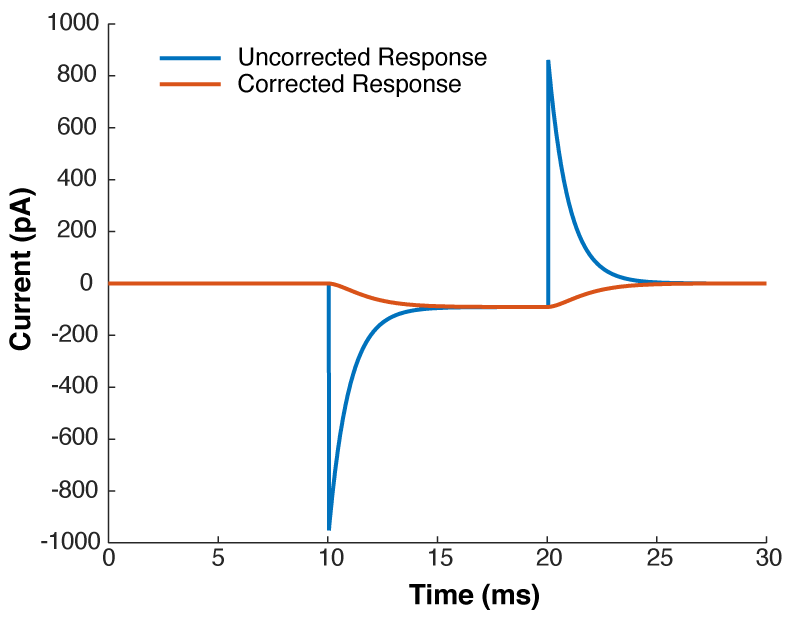
This doesn’t do anything to improve your voltage clamp, but it does provide a little electrical help to the amplifier (See Note 1). More importantly however, it informs your amplifier what Rs and Cm are so that the series resistance compensation circuit can work.
Because of the fact that the Rs and Cm values you put into your amplifier are used for series resistance compensation, their exact values matter: If you over-estimate Rs, the Vm of the cell will be pushed further from the resting membrane potential than you expect. If you over estimate Cm, the voltage of the cell will oscillate before settling at a final value.
Despite the importance of setting the Rs and Cm values on your amplifier, I’ve never seen a guide on how to actually do it. If you patch HEK-293 cells, or N1E-115s, it’s simple: either slowly increase Rs and Cm together, and you will eventually zero in on the correct values. Or, slightly more scientifically, estimate Rs by dividing the size of the voltage step you are applying by the peak amplitude of the capacitive transient, dial that in and then increase Cm until you are left with a smooth rising curve like that shown in Fig 1. (you’ll probably need to do some slight adjustment of Rs to get it perfect). However, in neuron with dendrites, things are not quite so simple.
You see, when you set the whole-cell parameters, all the amplifier does is subtract off the current needed to charge a capacitor through a resistor with values equal to the Cm and Rs values you have entered on the amplifier. Want to see what I mean?
The current through a capacitor and resistor in series is described by this equation:
$latex I = \frac{ V_{cmd} }{R_{s}}e^{\frac{-t}{R_{s}C_{m}}} &s=3$
So we can calculate that current, and mathematically subtract it from the response to out test pulse, and we should end up with what we saw in figure 1. Look at figure 2 below, that’s exactly what I’ve done. The blue line is the raw trace, the orange line was calculated with the equation above, and when I take the difference of those two lines I end up with the yellow curve, which looks almost exactly like what we saw in figure 1.
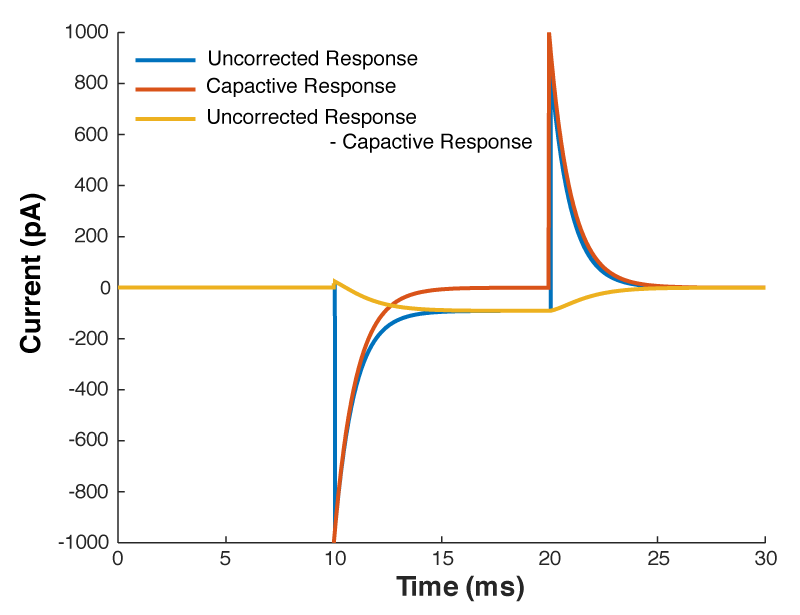
But what all of this means is that if your cell isn’t made up of a capacitor with the value you have entered, and/or that capacitor isn’t being charged through a resistor of the size you have entered, then you’re going to be in trouble. And you’re nearly always going to be in trouble if you’re patching a real neuron as they can never be explained by a single capacitor. And that means that no matter how you set Rs and Cm on your amplifier, you can never get the current to look like what you see in Fig 1. Instead, it looks like Fig 3.
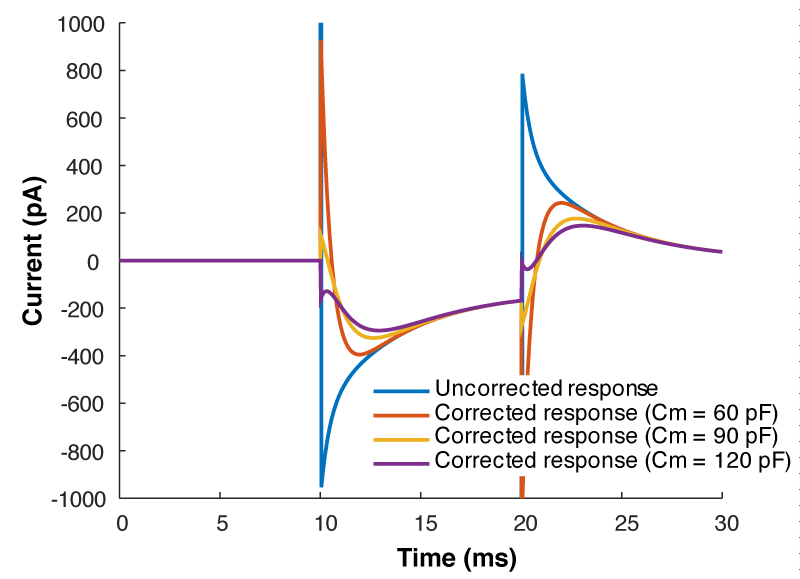
What is going on here? Why can’t you get a textbook response in your current when you patch a neuron? Well as I said above, when you dial in your whole cell parameters, you are just subtracting off the response of a capacitor being charged through a resistor. However, a real cell with dendrites can’t be described by a single capacitor, it has dendritic compartments with capacitance, and the dendritic capacitance doesn’t just add to the somatic capacitance because the dendrite is hidden behind the resistance of the cytoplasm down the dendrite (which acts exactly like another series resistor). Because of that, it is impossible to get the waveform to look like figure 1. So how should the waveform appear to let you know you have correctly dialed in the whole cell parameters?
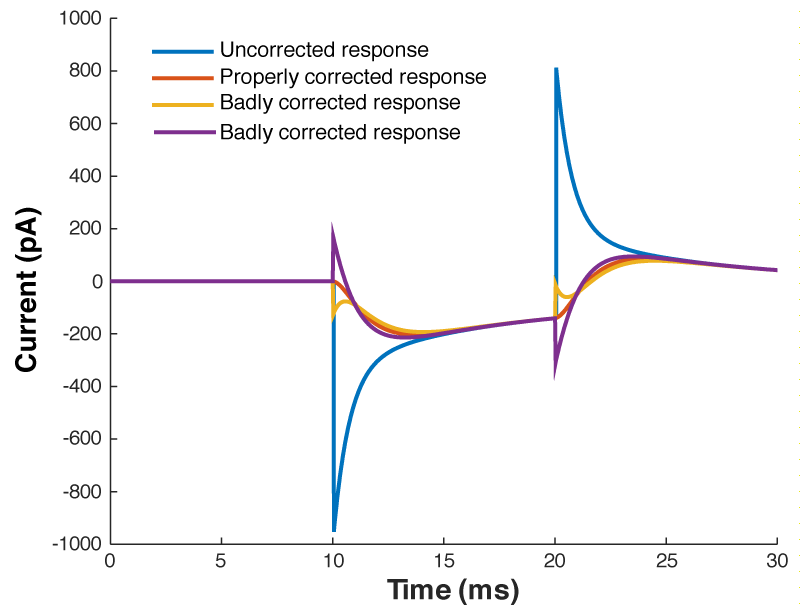
Figure 4 shows a properly corrected response along with two bad examples. I’ve seen people incorrectly dial in Cm and Rs in a futile attempt to get the waveform to look like a textbook response, and it usually looks like the purple and yellow traces. People think that they want a fast rising response, so over set Rs to get a squarish looking step. Yes, you do want a fast rising response, but you achieve this by ACTUALLY lowering Rs, not by mis-setting Rs on the amplifier. I’ve also seen people underset Cm in order to make the response look more square. This can be especially easy to do if you have aggressive low pass filtering (e.g. 1 kHz) as it will clip off where the current goes in the wrong direction (i.e. the positive going current at the start of the step). What you’re looking for is a smooth rise from the holding current when your test pulse starts, and you shouldn’t worry yourself about the departure from squareness as there is nothing you can do about it. The approach of calculating Rs from the peak size of the capacative transient, and then dialing in Cm until the transient disappears is still the best approach.
So do you want to see what this looks like in real life? [All the above graphs were generated in NEURON]. Thankfully I made some recordings where I made dual whole-cell recordings from a single soma. One electrode was in voltage clamp and the other was in current clamp. This allows the electrode in current clamp to measure exactly how our voltage clamp was performing. In the below waveforms, the current trace from the electrode in voltage clamp is on top (Ihold) and the membrane potential is shown on the bottom. The voltage clamp is attempting to make a voltage step from -70 mV to – 80mV. I have turned on 70% series resistance compensation which will then demonstrate the effect of incorrectly applying whole-cell correction.
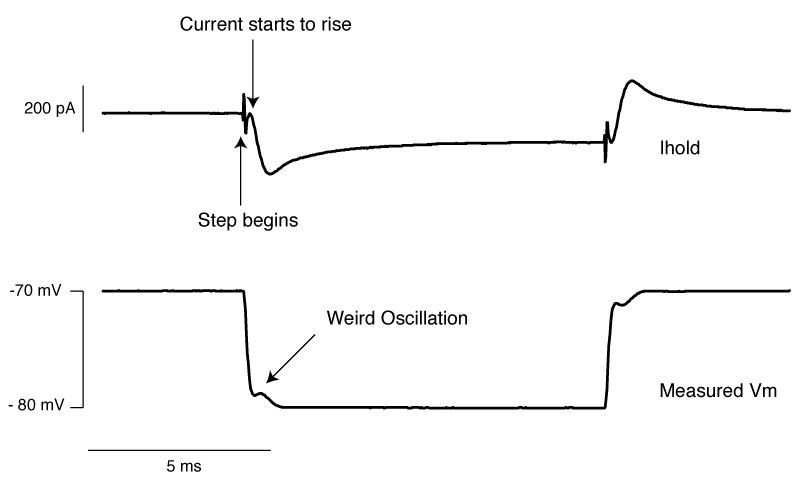
The above shows us a very common mistake. Everything about the current response looks right, apart from one crucial detail: the current starts to rise several 100 microseconds after the step truly begins. This means that the whole cell capacitance is over set, and it leads to a little oscillation in the voltage response.
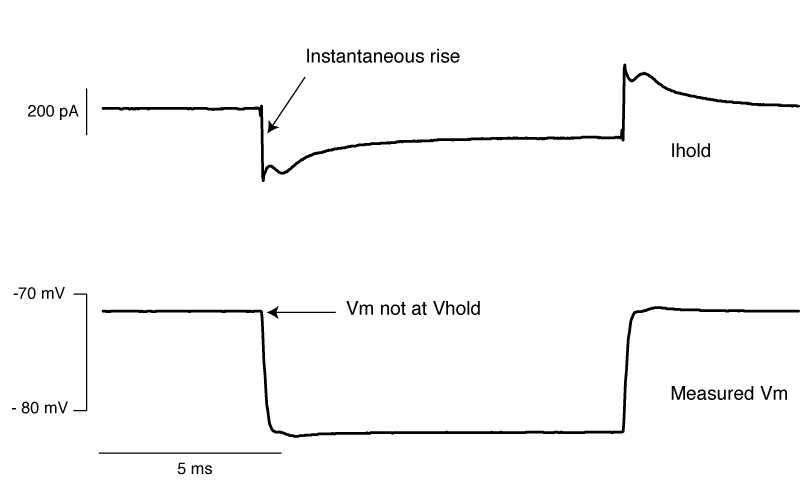
The above is what it looks like when you overset Rs. The only time I’ve seen this in the wild is when the true series resistance into a cell randomly drops without anyone noticing. . You can see the current response shows an instantaneous rise. By oversetting Rs, the series resistance compensation is over doing things, and hence despite met telling the amplifier to clamp the cell at -70 mV, we’re actually at about -72 mV. Likewise, the step amplitude is larger than -10 mV. A 1 mV error is really nothing to worry about, but it’s better to avoid it if you can.
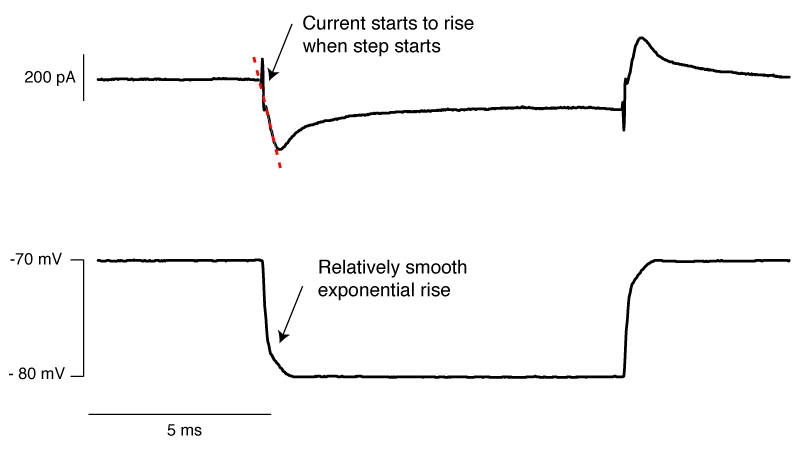
Finally, we have an approximately correctly set example. The important thing to note is that if you extrapolate backwards from when the rising phase of the transient, it intersects with the baseline current at the moment the voltage step begins (red dashed line). In this particular instance, there is a small instantaneous rise, but this is probably the remnants of uncompensated pipette capacitance. When you are there doing it for real, and you’re looking for this point where the extrapolated current intersects with baseline, it’s pretty easy to tell the difference between a little bit of pipette capacitance and big instantaneous rise shown in figure 6.
So, in conclusion:
- When you perform whole-cell correction, i.e. dial in the series resistance and whole-cell capacitance, you are NOT improving your voltage clamp, you are just subtracting off the current needed to charge the membrane capacitor.
- However, it is important to perform whole-cell correction properly as the values you determine are used to perform series resistance compensation.
- Your best approach is to estimate the series resistance by dividing the size of your test pulse in mV by the peak amplitude of the capactive transient. Then dial that in and start increasing the whole-cell capacitance until the extrapolation of the remaining transient looks like it intersects the holding current at the moment the test pulse starts.
Note 1. When you are performing voltage clamp, you often need to step the cell you’re recording from to a new voltage. When you do this, you need to charge up the capacitance of the cell membrane. Your ability to charge up this membrane capacitor is limited by the resistance of your electrode and the junk in its tip from when you went whole-cell, i.e. your series resistance (Rs). The lower the Rs, the more current your can pump into your cell, and the faster the membrane potential (Vm) approaches your command potential (Vcmd). While you essentially always want as low Rs as possible, it a low Rs can come with a downside: that initial inrush of current when you try to step the potential can saturate certain electronics inside the amplifier (the primary operational amplifier responsible for voltage clamp). When you correct for whole cell parameters, you pass the job of charging up the membrane capacitor to another operational amp, freeing up the primarily operational amplifier to pass current in response to ion channels. Not only does this minimize the risk of saturating the primarily amplifier, but the values are used to perform series resistance compensation.
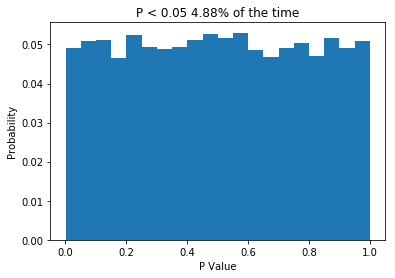
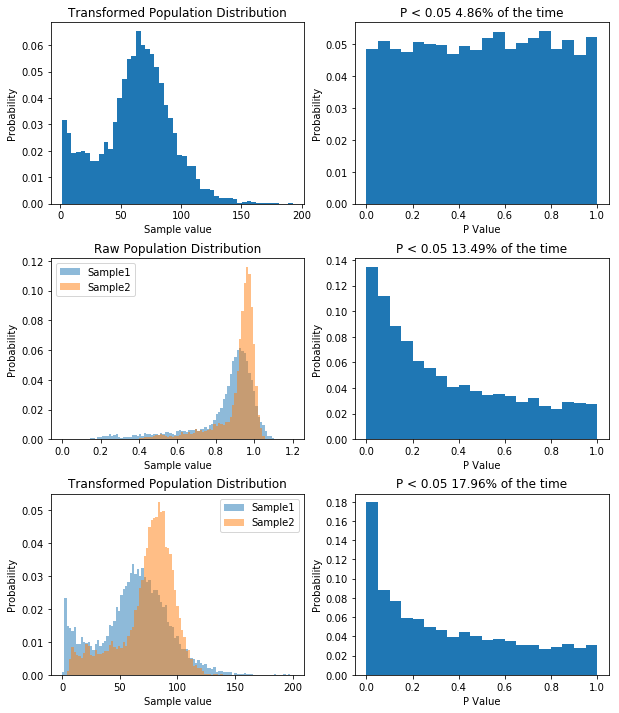
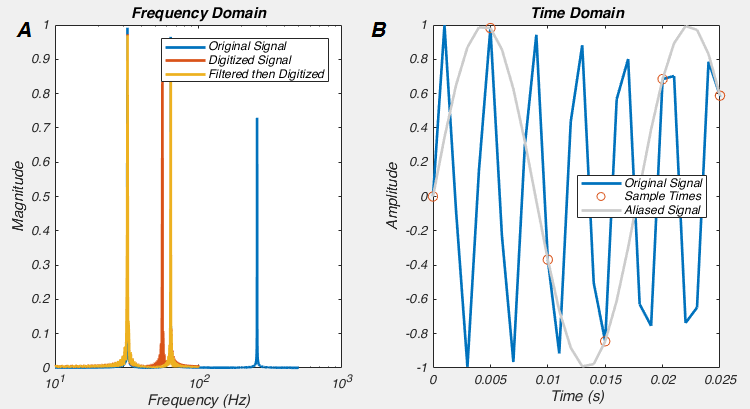
]]>So I want to preface this post by saying that I don’t have a degree in biostatistics. However, this post relies on a fact that I’m pretty comfortable stating: If the null hypothesis is true (e.g. there is no difference between your populations), then P should only be less than 0.05 5% of the time. That’s half the point of null-hypothesis statistical testing! Lets write some quick python code to demonstrate this.
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(1) #set random seed so you get same data
n_reps = 10000 #perform 10000 times
ps = np.zeros(n_reps)
for n in range(n_reps):
#make two normally distributed samples, with mean=0, std dev = 1 and n = 10
sample1 = np.random.normal(loc = 0, scale = 1, size = 10)
sample2 = np.random.normal(loc = 0, scale = 1, size = 10)
#perform t test
(t, ps[n]) = stats.ttest_ind(sample1, sample2)
weights = np.ones_like(ps)/float(len(ps))
plt.hist(ps, bins = 20, weights = weights)
plt.xlabel('P Value')
plt.ylabel('Probability')
plt.title('P < 0.05 ' + str(np.sum(ps<0.05)/float(len(ps))*100) + '% of the time')
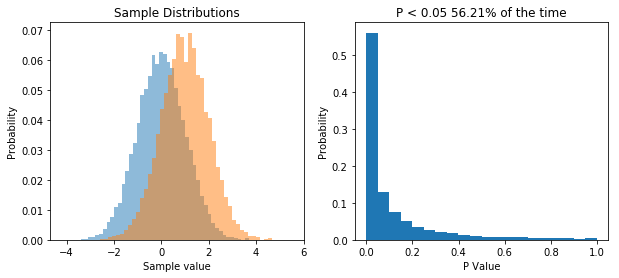
So what we do is create two normally distributed random variables, which have the same mean, the same standard deviation and n = 10, we subject them to a t-test, and we repeat this 10,000 times. Because the two samples are drawn from the same distribution, we would expect no difference between them, and the P values we get support that idea: getting P values less than 0.05 are relatively rare. In fact, the P value is less than 0.05 about 5% of the time, which is what leads people to say (incorrectly) that “if we reject the null hypothesis when P < 0.05, then we will only be wrong 5% of the time”. The important thing is that when testing samples where you know the null hypothesis is true, the P value should be uniformly distributed. If that is not the case, something is wrong. So what about when the null hypothesis isn’t true? Let’s change the code a little and see.
np.random.seed(1) #set random seed so you get same data
n_reps = 10000 #perform 10000 times
ps = np.zeros(n_reps)
for n in range(n_reps):
#make two normally distributed samples, with mean=0 or 1, std dev = 1 and n = 10
sample1 = np.random.normal(loc = 0, scale = 1, size = 10)
sample2 = np.random.normal(loc = 1, scale = 1, size = 10)
#perform t test
(t, ps[n]) = stats.ttest_ind(sample1, sample2)
fig, ax = plt.subplots(1, 2, figsize=(10,4))
weights = np.ones(10000)/float(10000)
ax[0].hist(np.random.normal(loc = 0, scale = 1, size = 10000), bins = 50, weights = weights, alpha = 0.5)
ax[0].hist(np.random.normal(loc = 1, scale = 1, size = 10000), bins = 50, weights = weights, alpha = 0.5)
ax[0].set_xlabel('Sample value')
ax[0].set_ylabel('Probability')
ax[0].set_title('Sample Distributions')
weights = np.ones_like(ps)/float(len(ps))
ax[1].hist(ps, bins = 20, weights = weights)
ax[1].set_xlabel('P Value')
ax[1].set_ylabel('Probability')
ax[1].set_title('P < 0.05 ' + str(round(np.sum(ps<0.05)/float(len(ps))*100,2)) + '% of the time')
So now we repeatedly perform a t-test on two samples drawn from two different populations. What we see is that now the distribution of P values is skewed, and P is less than 0.05 about 56% of the time, meaning that we have a power of 56% to detect the difference between the two populations given our sample size.
The point I want to get across is that the distribution of P values is uniform when the null hypothesis is true, and it’s skewed when the null hypothesis is false.
So now what happens if our data isn’t drawn from a normal distribution? Well let’s change our code again and see.
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(1) #set random seed so you get same data
n_reps = 10000 #perform 10000 times
ps = np.zeros(n_reps)
for n in range(n_reps):
#make two log normally distributed samples from the same population.
sample1 = np.random.lognormal(mean = 2, sigma = 1.5, size = 10)
sample2 = np.random.lognormal(mean = 2, sigma = 1.5, size = 10)
#perform t test
(t, ps[n]) = stats.ttest_ind(sample1, sample2)
fig, ax = plt.subplots(1, 2, figsize=(10,4))
#plot the distribution out data was sampled from
ax[0].hist(np.random.lognormal(mean = 2, sigma = 1.5, size = 1000), bins = 50)
ax[0].set_xlabel('Sample value')
ax[0].set_ylabel('Frequency')
ax[0].set_title('Sample Distribution')
weights = np.ones_like(ps)/float(len(ps))
ax[1].hist(ps, bins = 20, weights = weights)
plt.xlabel('P Value')
plt.ylabel('Probability')
plt.title('P < 0.05 ' + str(np.sum(ps<0.05)/float(len(ps))*100) + '% of the time')
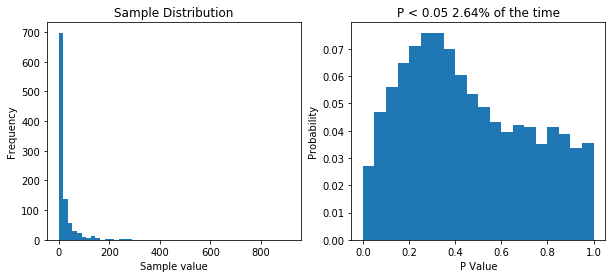
So now our samples are drawn from a lognormal distribution with a heavy positive skew. When we perform 10,000 t-tests we see that our distribution of P values is no longer uniform. This tells us that something isn’t right. But does it means we’re more likely to make type I error (rejecting the null hypothesis when we shouldn’t/false positive) or a type II error (accepting the null hypothesis when we shouldn’t/false positive). Well our simulation tested a case where the null hypothesis was true (i.e. there was no difference) and we would reject the null hypothesis when P is less than 0.05. Now P is less than 0.05 about 2.5% of the time, so our type I error rate has actually gone down. But what about the type II error rate? Well we need to run another simulation to see.
np.random.seed(1) #set random seed so you get same data
n_reps = 10000 #perform 10000 times
norm_ps = np.zeros(n_reps)
log_ps = np.zeros(n_reps)
mean1 = 1
mean2 = 2
variance = 1
for n in range(n_reps):
#make two normally distributed samples, with mean=0, std dev = 1 and n = 10
norm_sample1 = np.random.normal(loc = mean1, scale = np.sqrt(variance), size = 10)
norm_sample2 = np.random.normal(loc = mean2, scale = np.sqrt(variance), size = 10)
log_sample1 = np.random.lognormal(mean = np.log(mean1/np.sqrt(1+variance/mean1**2)), sigma = np.sqrt(np.log(1+variance/mean1**2)), size = 10)
log_sample2 = np.random.lognormal(mean = np.log(mean2/np.sqrt(1+variance/mean2**2)), sigma = np.sqrt(np.log(1+variance/mean2**2)), size = 10)
#perform t test
(t, norm_ps[n]) = stats.ttest_ind(norm_sample1, norm_sample2)
(t, log_ps[n]) = stats.ttest_ind(log_sample1, log_sample2)
fig, ax = plt.subplots(2, 2, figsize=(10,10))
weights = np.ones(10000)/float(10000)
ax[0,0].hist(np.random.normal(loc = 0, scale = 1, size = 10000), bins = 50, weights = weights, alpha = 0.5, label="Sample1")
ax[0,0].hist(np.random.normal(loc = 1, scale = 1, size = 10000), bins = 50, weights = weights, alpha = 0.5, label="Sample2")
ax[0,0].legend(prop={'size': 10})
ax[0,0].set_xlabel('Sample value')
ax[0,0].set_ylabel('Probability')
ax[0,0].set_title('Normal Population Distributions')
weights = np.ones_like(norm_ps)/float(len(norm_ps))
ax[0,1].hist(norm_ps, bins = 20, weights = weights)
ax[0,1].set_xlabel('P Value')
ax[0,1].set_ylabel('Probability')
ax[0,1].set_title('P < 0.05 ' + str(round(np.sum(norm_ps<0.05)/float(len(norm_ps))*100,2)) + '% of the time')
weights = np.ones(10000)/float(10000)
ax[1,0].hist(np.random.lognormal(mean = np.log(mean1/np.sqrt(1+variance/mean1**2)), sigma = np.sqrt(np.log(1+variance/mean1**2)), size = 10000), weights = weights, alpha = 0.5, bins = np.linspace(0,20,100), label="Sample1")
ax[1,0].hist(np.random.lognormal(mean = np.log(mean2/np.sqrt(1+variance/mean2**2)), sigma = np.sqrt(np.log(1+variance/mean2**2)), size = 10000), weights = weights, alpha = 0.5, bins = np.linspace(0,20,100), label="Sample2")
ax[1,0].legend(prop={'size': 10})
ax[1,0].set_xlabel('Sample value')
ax[1,0].set_ylabel('Probability')
ax[1,0].set_title('Lognormal Population Distributions')
weights = np.ones_like(log_ps)/float(len(log_ps))
ax[1,1].hist(log_ps, bins = 20, weights = weights)
ax[1,1].set_xlabel('P Value')
ax[1,1].set_ylabel('Probability')
ax[1,1].set_title('P < 0.05 ' + str(round(np.sum(log_ps<0.05)/float(len(log_ps))*100,2)) + '% of the time')
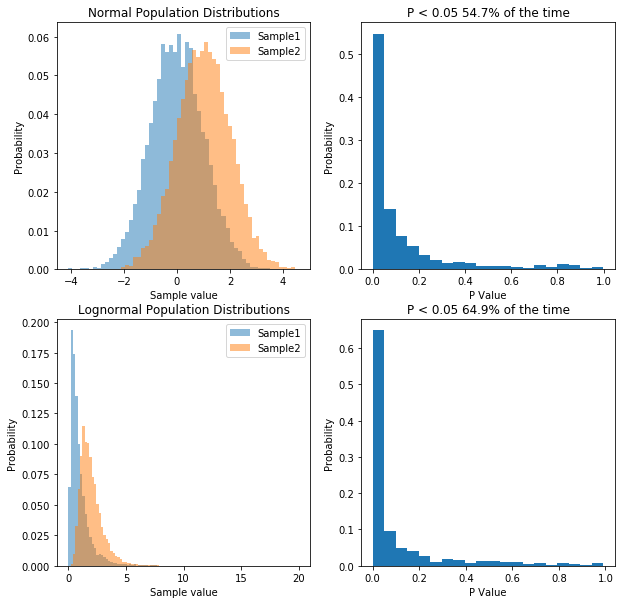
So what we’ve done is run 10,000 simulations of two experiments. In one we take samples from two normal populations, both with a standard deviation of 1, and means of 1 and 2 respectively. In the other, we take samples from two lognormal populations, again, with a standard deviation of 1, and means of 1 and 2 respectively. As before, when we sample from a normal distribution, our t-test has a power of about 55%. However, in the case of our lognormal distribution we end up with a power of 65%. So does that mean people have been lying to you, and that doing statistics on non-normal data is actually better?. That would be the wrong conclusion, because if we transform the data, we can get even higher power. Specifically, if we log our lognormal data, and make it normally distributed, our power goes up significantly. Check it out:
np.random.seed(1) #set random seed so you get same data
n_reps = 1000 #perform 10000 times
norm_ps = np.zeros(n_reps)
log_ps = np.zeros(n_reps)
mean1 = 1
mean2 = 2
variance = 1
for n in range(n_reps):
log_sample1 = np.log(np.random.lognormal(mean = np.log(mean1/np.sqrt(1+variance/mean1**2)), sigma = np.sqrt(np.log(1+variance/mean1**2)), size = 10))
log_sample2 = np.log(np.random.lognormal(mean = np.log(mean2/np.sqrt(1+variance/mean2**2)), sigma = np.sqrt(np.log(1+variance/mean2**2)), size = 10))
#perform t test
(t, log_ps[n]) = stats.ttest_ind(log_sample1, log_sample2, equal_var=False)
fig, ax = plt.subplots(1, 2, figsize=(10,4))
weights = np.ones(10000)/float(10000)
ax[0].hist(np.log(np.random.lognormal(mean = np.log(mean1/np.sqrt(1+variance/mean1**2)), sigma = np.sqrt(np.log(1+variance/mean1**2)), size = 10000)), weights = weights, alpha = 0.5, bins = np.linspace(-4,4,100), label="Sample1")
ax[0].hist(np.log(np.random.lognormal(mean = np.log(mean2/np.sqrt(1+variance/mean2**2)), sigma = np.sqrt(np.log(1+variance/mean2**2)), size = 10000)), weights = weights, alpha = 0.5, bins = np.linspace(-4,4,100), label="Sample2")
ax[0].legend(prop={'size': 10})
ax[0].set_xlabel('Sample value')
ax[0].set_ylabel('Probability')
ax[0].set_title('Log(Lognormal Population Distributions)')
weights = np.ones_like(log_ps)/float(len(log_ps))
ax[1].hist(log_ps, bins = 20, weights = weights)
ax[1].set_xlabel('P Value')
ax[1].set_ylabel('Probability')
ax[1].set_title('P < 0.05 ' + str(round(np.sum(log_ps<0.05)/float(len(log_ps))*100,2)) + '% of the time')
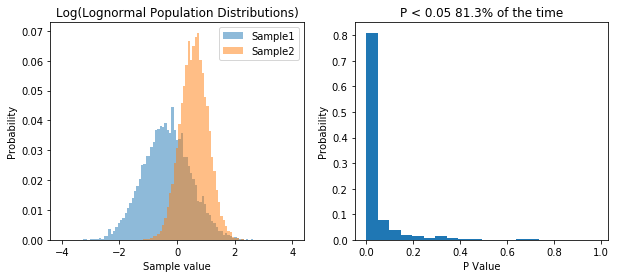
So transforming the data to make it normal has increased our power. So basically, working with lognormal data decreases our type I error rate, but INCREASES our type II error rate, relative to normal data.
Okay, so now we know how to see what kind of effect sampling simulated data from perfect distributions has on our statistics. But can we look at our own data and get an idea of how much of an effect it’s non-normality will have on our results? Normality tests like the Anderson-Darling test aren’t much use here. If your sample size is small, normality tests will nearly always tell you you data is normal, and if your sample size is large, even negligible deviations from normality will cause the test to tell you that your data is not normal. In reality, we don’t want a test to tell you whether your data is exactly, perfectly normal. You want to know whether its deviations from normality matter. So what we can do instead is generate a simulated population that matches our data, then draw random samples from it. Thankfully this is actually pretty easy to in python, though it does require a bit of care.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity
data = np.array([0.9390851, 0.9666265, 0.7483506, 0.9564947, 0.243594, 0.9384128, 0.3984024, 0.5806361, 0.9077033, 0.9272811, 0.9013306, 0.9253298, 0.9048479, 0.9450448, 0.8598598, 0.8911161, 0.8828563,0.9820026,0.9097131,0.9449918,0.9246619,0.9933545,0.8525506,0.791416,0.8806227,0.8839348,0.8120107,0.6639317,0.9337438,0.9624416,0.9370267,0.9568143,0.9711389,0.9332489,0.9356305,0.9160964,0.6688652,0.9664063,0.4913768]).reshape(-1,1)
x = np.linspace(-1, 2, 100).reshape(-1,1)
fig, ax = plt.subplots(1,3, figsize=(10,4), sharey=True)
bw = [0.25, 0.05, 0.01]
ax[0].set_ylabel('Normalized PDF')
for n in range(ax.size):
#Create our estimated distribution
kde = KernelDensity(kernel='gaussian', bandwidth=bw[n]).fit(data)
#Plot our estimated distribution
plt.sca(ax[n])
ax[n].fill(x, np.exp(kde.score_samples(x))/np.max(np.exp(kde.score_samples(x))), '#1f77b4')
ax[n].plot(data, np.random.normal(loc = -0.05, scale = 0.01, size= data.size), '+k')
ax[n].set_xlim(-0.5, 1.5)
plt.xticks([0, 1])
ax[n].set_ylim(-0.1, 1.1)
ax[n].set_title('Bandwidth = '+str(bw[n]))
ax[n].set_xlabel('Sample value')
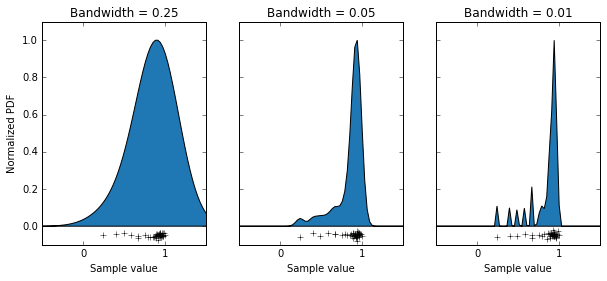
What we’ve done is use the KernelDensity function from the scikitlearn package, which generates a probability density function by summing up lots of little functions AKA a kernel, where each data point is. The choice of an appropriate kernel is key to generating a good probability density function. In this case we’ve chosen a Gaussian kernel, but we can still alter it’s “bandwidth” (basically it’s standard deviation). I have some data that is the orientation selectivity index of some axon terminals (the data points along the bottoms of the graphs). This measure can only take on values between 0 and 1. We can see that using a bandwidth of 0.25 has done a bad job of modelling our population, as it’s saying values above 1 are quite likely, and that the distribution is basically symmetrical. Using a bandwidth of 0.01 has also done a bit of a bad job, as you can see it’s made a multi-modal distribution, which I’m pretty sure isn’t accurate. Using a bandwidth of 0.05 seems to have done a pretty good job, producing a relatively smooth curve which seems to model out data well. So with that decided, let’s use that probability density function to sample some data, and do some t-tests when the null hypothesis is true
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.neighbors import KernelDensity
np.random.seed(1) #set random seed so you get same data
n_reps = 10000 #perform 10000 times
ps = np.zeros(n_reps)
data = np.array([0.9390851, 0.9666265, 0.7483506, 0.9564947, 0.243594, 0.9384128, 0.3984024, 0.5806361, 0.9077033, 0.9272811, 0.9013306, 0.9253298, 0.9048479, 0.9450448, 0.8598598, 0.8911161, 0.8828563,0.9820026,0.9097131,0.9449918,0.9246619,0.9933545,0.8525506,0.791416,0.8806227,0.8839348,0.8120107,0.6639317,0.9337438,0.9624416,0.9370267,0.9568143,0.9711389,0.9332489,0.9356305,0.9160964,0.6688652,0.9664063,0.4913768]).reshape(-1,1)
x = np.linspace(-1, 2, 100).reshape(-1,1)
kde = KernelDensity(kernel='gaussian', bandwidth=0.05).fit(data)
for n in range(n_reps):
sample1 = kde.sample(10)
sample2 = kde.sample(10)
(t, ps[n]) = stats.ttest_ind(sample1, sample2)
fig, ax = plt.subplots(1, 2, figsize=(10,4))
#plot the distribution out data was sampled from
weights = np.ones(10000)/float(10000)
ax[0].hist(kde.sample(10000), bins = 50, weights = weights)
ax[0].set_xlabel('Sample value')
ax[0].set_ylabel('Probability')
ax[0].set_title('Population Distribution')
weights = np.ones_like(ps)/float(len(ps))
ax[1].hist(ps, bins = 20, weights = weights)
plt.xlabel('P Value')
plt.ylabel('Probability')
plt.title('P < 0.05 ' + str(np.sum(ps<0.05)/float(len(ps))*100) + '% of the time')
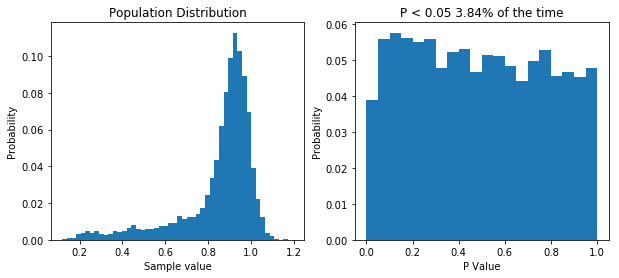
Simulating our non-normal data allows us to show that we’d almost half our type I error rate if we used it.
So like when we were dealing with non-normal data before, our type I error rate has gone down. So you can bet our type II error rate is higher than it needs to be. But let’s prove it. First, I think that transforming our data by taking a large number, say 100, and raising it to the power of our data will make the data more normal. If that’s true, out P value distribution in the null case should be more uniform, and the power in the non-null case should be higher. I’ll spare you the code, though it’s available here. But the result is what I predicted, as you can see below.
So by applying our transform we’ve seen how having non-normal data decreases our type I error rate, but increases our type II error rate. For what it’s worth, with the kind of data I had, trying to transform it to normality was a bad idea, as it will never become normal, and I’d be better off using a different model altogether, but the underlying concept remains: you can use KernelDensity to allow you to draw data from your own distribution.
Finally, there is one more thing I want to cover. Some statisticians like to point out that when performing good old fashioned t-tests and ANOVAs, there is no assumption of normality: the data can follow any distribution and hypothesis testing will be legitimate. In certain cases, this is true. Specifically, if the sample size is big enough, even wildly non-normal data will behave well in parametric tests. However, even with relatively tame non-normal data, the number of samples require before the t-test is well behaved can be very large, well outside the range that most physiologists will be able to achieve. The figure below shows that. I’ve done what I’ve done before and performed 10,000 t-tests on data from the same population, with varying sample sizes. Even with a sample size of 100, the distribution of p values isn’t uniform.
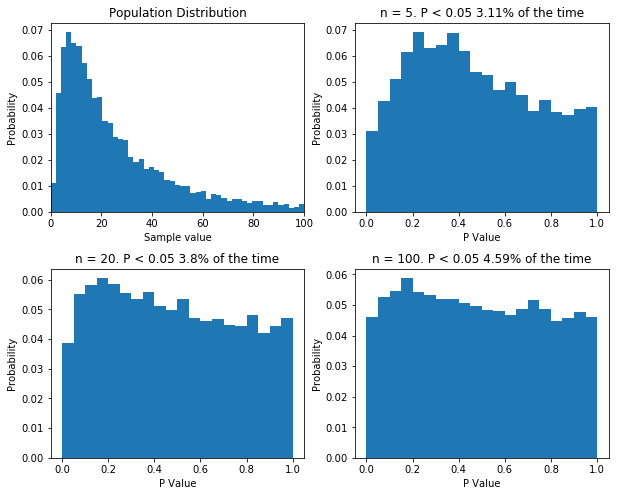
If your sample size is large enough, classical null-hypothesis statistical testing is well behaved with non-normal data. But the sample size might need to be very large. Even with n = 100, the distribution of p values in the null case is not uniform.
I should point out that there are a bunch of caveats here. For instance, if you’re the first person to measure something, and you have n = 5, then you probably can’t usefully use KernelDensity to construct a population distribution, as you have no idea what it looks like. For much the same reason, you can’t use the techniques I’ve demonstrated to measure the power of your hypothesis testing based on your samples: power analysis relies on know population variables, not sample variables… There are probably other caveats, I’ll let you know once people on twitter tell me.
So in conclusion, if hypothesis testing is working properly, when the null hypothesis is true, P values should be uniformly distribution. If the null hypothesis is not true the distribution of P values is skewed. For P values to mean what you think they mean, when you perform standard t-tests and ANOVAs your data needs to be normally distributed unless you have very large sample size. With a bit of care you can use KernelDensity to simulate your population of interest. Then you can perform t-tests on the null-hypothesis to simply look at your type I error rate. And so long as you have a way of transforming your data to make it normal, you can then see what effect doing analysis on your untransformed data has on your type II error rate. Often you don’t know how to transform your data to make it normal and that is why simulating the null hypothesis is so useful.
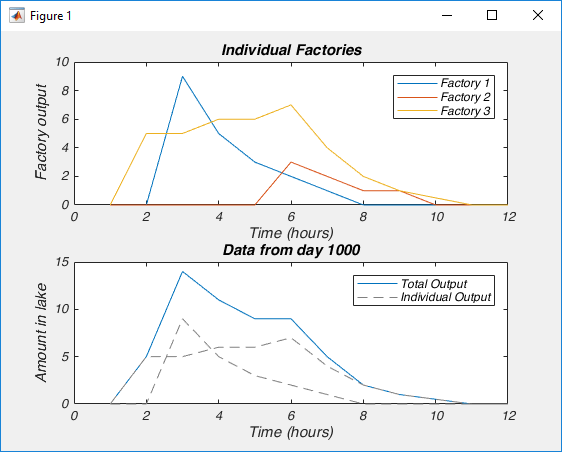
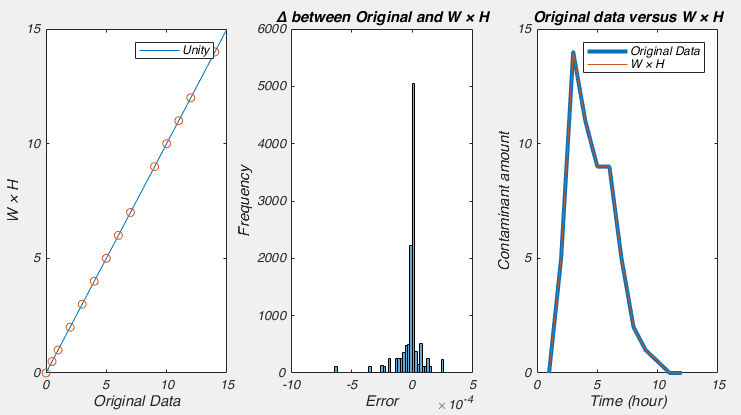
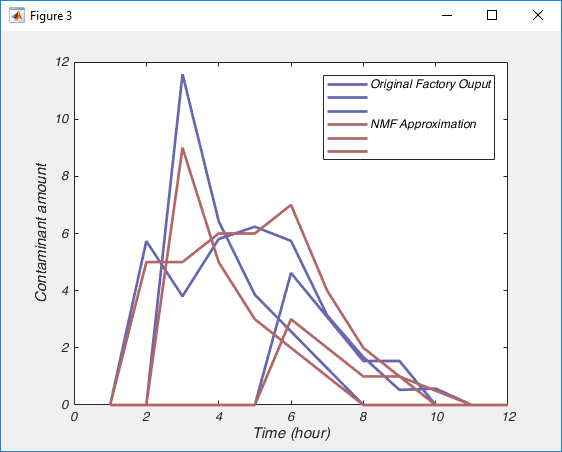
So Nonnegative Matrix Factorization (NMF) can be explained in a variety of ways, but I think the simplest way is that NMF reveals your signal’s component parts. That is to say, if your signal is the sum of a variety of other signals, then NMF will reveal those underlying signals. To me, this naturally makes me think of signals that vary over time, but NMF can be used on a variety of other signals, like images, or text. However, in order to get to the examples, we need to understand how NMF works. So lets break NMF down, word by word. (If you’re fine with the concepts of matrix multiplication and factorization, skip down to “Example 1 – Time series“).
Nonnegative
This is the easiest bit to explain. NMF only works on signals that are always positive. I’ve said that NMF splits a signal up into the individual elements that are summed up to make the signal. Because the signal must always be positive, the individual elements must also be positive. However, you can take a negative signal, add some positive value to it and it becomes positive. So then you can use NMF on it, right? Well not always. What is more important to think about is the individual elements. To make your signal, are the individual elements always added together, or is one element subtracted from another? If it is the former, then NMF may work, even if the signal is always negative (once you add a constant to the data to make it positive). If it is the later, NMF will never work. For example, lets say we were interested in the amount of a contaminant in lake. Every day various factories dumped discharge into the lake. Perhaps we could use NMF to figure out how each factory affected the amount of contaminant in the lake (because the total contaminant is a sum of all the discharges from each factory). However, if the lake was sometimes cleaned of the contaminant, NMF probably isn’t appropriate, as we now have a subtractive signal mixed in with our additive signal.
Matrix
Even the word “matrix” may intimidate some people. There is nothing magical about matrices. They are just a collection of numbers arranged in a square/rectangle. And just like there are rules for how you multiply numbers, there are rules for how you multiply matrices, rules that you need to understand in order to understand NMF. While these rules may seem a little weird if you’re only used to multiplying numbers, thankfully, they’re not very difficult to remember. It’s easiest to just see the rules in action. Concretely, if we have two matrices, X and Y where:
X = \begin{bmatrix}
3 & 1 \\
2 & 5 \\
\end{bmatrix}
,
Y = \begin{bmatrix}
4 & 2 \\
2 & 1
\end{bmatrix}
&s=1$
Then we calculate X × Y by doing the following
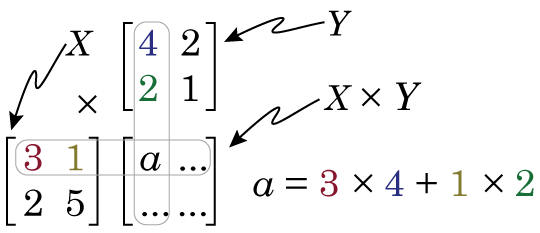
So if we look at element a in the product matrix X × Y (i.e. the number in first column, first row), we see it is somehow related to the first row of matrix X, and the first column of matrix Y. We see that the first element in the first row of matrix X is multiplied by the first element in the first column of matrix Y, and this is added to the product of the second element in the first row of matrix X and the second element in the first column of matrix Y. It’s worth noting at this point that this means that X × Y produces a matrix that is NOT the same as Y × X.
If you’ve never come across matrix multiplication before, this may all seem very strange, very pointless and very annoying. But let me show one way of thinking of matrix multiplication that hopefully will make it make some sense, or at least give it some utility. Let us say that matrix X is some data, we can then see matrix Y and set of weights, where X × Y is now a sort of weighted average of X. How does this work? Well, if the first row of X is a set of obervations, then the first column of Y is our weights. As we move across the elements in that row of X (our data), we look to the corresponding element in the column of Y (our weights), and multiply the two together. If the element in Y is large, then that element of X is amplified. If the element in Y is zero, then that element of X is ignored. But lets look at a concrete example. We have matrices X and Y,
X = \begin{bmatrix}
3 & 1 \\
2 & 5 \\
\end{bmatrix}
,
Y = \begin{bmatrix}
1 & 2 \\
0 & 1
\end{bmatrix}
&s=1$
and we multiply them together:
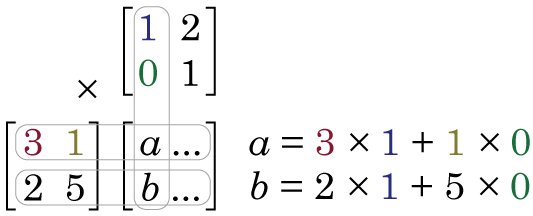
Because the first element of the first column of Y is 1, we then apply this weighting to the first element of the first row of X. However, the second element of the first column of Y is zero. This means we apply a zero weight to second element of the first row of X. We sum these two products (3 × 1 + 1 × 0 = 3) and we put the result in the first row, first column of X × Y. When we go down to the second row of X, we again apply the weights of the first column of Y, and the element in the second row, first column of X × Y is 2 × 1 + 5 × 0 = 2. Notice, because the first column of Y was [1 0] now the first column of X × Y is [3 2], i.e. we applied a weighting of 1 to the first column of X, and a weighting of zero to the second column, and so we just reproduced first column of X. In order to calculate what will be in the second column of X × Y, we apply the weights see in the second column of Y, to the data in X.
So to put this really succinctly, the element in the ith row, jth column of the matrix X × Y is the data in the ith row of X, weighted by the weights in the jth column of Y. If any element, say element n, in the jth column of Y is much much larger than all the other elements in that column, then then jth column of X × Y will essentially be equal to the nth column of X, multiplied by the value of that nth element in Y. I’m going restate that idea again, because it is super important later on: As we travel down a column in Y, if any element is much much larger than all the others, then that same column of X × Y will be essentially equal to the equivalent column of X, multiplied by a constant.
This may all be a lot to take in, so as hopefully a simple exercise that will help you see how when you calculate X × Y, Y acts like a set of weights. What is the product of these two matrices:
\begin{bmatrix}
8 & 1 & 6 \\
3 & 5 & 7 \\
4 & 9 & 2
\end{bmatrix}
\times
\begin{bmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{bmatrix} = ?
&s=1$
Factorization
Hopefully you haven’t completely forgotten high school math, but if you have, factorization is solving this problem: if we have a number a, what are all the values of x and y such that x × y = a. So, the factors of the number 4 are 1, 4 and 2, as 1 × 4 = 4, and 2 × 2 = 4. These are strictly speaking, the positive integer factors of 4. There are an infinite number of non-integer factors, e.g. 0.25 × 16 = 4, -0.1 × -40 = 4 etc… We can factor matrices just the same. The factors of matrix Z are all the matrices such that X and Y such that X × Y = Z. And just like factorizing numbers, there can be a large number of factors for a given matrix, even an infinite number. But if you’re new to matrices there is a reason that there can be a large number factors for a given matrix that might not be immediately obvious: size.
If our matrix Z is 2 x 2 matrix, what sizes can the factors of Z be? Well any size, so long as X has 2 rows, and Y has 2 columns, and the “inner dimension” of X and Y match (“inner dimension” is the number of columns X has and the number of rows Y has) there may be factors of any size, see:
Matrix factorization (sometimes called “decomposition”) is a complex field, there are tonnes of approaches to factor matrices, with different goals and applications, but the different ways of factorizing a matrix all do fundamentally the same thing, you give it a matrix, and it gives you two (or more) matrices, that when multiplied together give you your original matrix or close approximation to it.
Approximation? How can you say two matrices are a factor of another matrix if it is only an approximation? Well it turns out a) factoring matrices is often very computationally complex b) some matrices don’t even have factors, especially given constraints like nonnegativity and c) an approximation is often good enough.
Alright, enough background, let’s get into how this works.
Example 1 – Time series
So earlier I gave a made up example: There are 3 factories that dump contaminants into a lake. Whether the factory dumps each day is random (so not all factories are active every day, in fact, if all factories were active every day, we couldn’t tease apart their signals). Each factory dumps a different amount of the contaminant with a different time course. We measure the concentration of the contaminant in the lake. We collect data for 1000 days. Can we figure out what each factories outflow looks like? With NMF we can.
First lets simulate our data:
rng(0);
%The output of each factory
factory1 = [0; 0; 9; 5; 3; 2; 1; 0; 0; 0; 0; 0];
factory2 = [0; 0; 0; 0; 0; 3; 2; 1; 1; 0; 0; 0];
factory3 = [0; 5; 5; 6; 6; 7; 4; 2; 1; 0.5; 0; 0];
%a matrix to store the all, for ease later on.
allfactories = horzcat(factory1, factory2, factory3);
num_days = 1000; % we collect data for 100 days
data = zeros(12,num_days); % preallocate matrix to store our data
h = figure();
set(h, 'MenuBar', 'none');
set(h, 'ToolBar', 'none');
subplot(2,1,1);
plot(allfactories);
xlabel('Time (hours)');
ylabel('Factory output');
legend('Factory 1', 'Factory 2', 'Factory 3');
title('Individual Factories')
for d = 1:num_days
which_factories = boolean(randi([0 1], 1, 3)); %Randomly decide which factory discharges today
output_for_day = sum(allfactories(:, which_factories), 2); %sum the output of active factories
data(:,d) = output_for_day;
end
subplot(2,1,2);
plot(output_for_day);
hold on;
plot(allfactories(:, which_factories), '--', 'Color', [0.5 0.5 0.5]);
hold off
xlabel('Time (hours)');
ylabel('Amount in lake');
legend('Total Output', 'Individual Output');
title('Data from day 1000')
Which should make a figure like this, where on the top we have the output of each factory, and on the bottom we have the concentration of contaminant in the lake on an arbitrary day, and how each factory contributed (only two factories dumped that day).
Now we’re going to do our NMF. It’s VERY important to think about this carefully. We need to lay our data out right, or the output of your NMF will be garbage. Specifically, each column of our data matrix needs to be a single observation, while each row of our matrix is the same data from a different observation. So in our example, each column is data from a different day, and each row is a different hour.
Why this is so crucial is that we can only understand the matrix factorization if we understand the data. Specifically, if we organize the data in this way, then when we factorize our data matrix such that W × H = Data, then the columns of W make up our signals that sum to make our data, and H make up our weights (in NMF, the factors are always called W and H, and I don’t know why). Have a look at this figure, and maybe re-read the section on matrix multiplication if you don’t see why.
Running NMF is simply a one line command in MATLAB.
[W, H] = nnmf(data, 3, 'replicates', 100);
Let’s just go over the one line in detail, we are saying we want to perform NMF on the matrix data, and return the factors W and H. The second argument 3 is stating how many individual signals we are trying to break the data down into. In our example, we know there are three factories. So we know 3 is a good number. Sometimes in real life, you wont know what value to use here, and it’s beyond the scope of this article to talk about how to choose values. The second and third argument is a parameter-value pair, where I am telling the algorithm to perform the factorization 100 times, and then choose the best one. This can be important. NMF is solved numerically, with the computer first having a random guess at the solution, and then iteratively improving it. Depending on that first guess, the final solution can vary significantly. Hence it is important to have many initial guesses and only choose the best solution.
So we run that line and what do we expect? W×H should equal our data, H should be a matrix filled with 0s and 1s, and the matrix W should be identical to our matrix allfactories. Why? Well W×H should equal our data because that is the whole point of NMF: finding two matrices that when multiplied together make our data. We expect H to be full of 0s and 1s, because those are the weights which say on a given day (column) which factories were dumping. Finally, we expect W to be equal to allfactories, as allfactories is a matrix containing the possible outputs of each factory, i.e. the individual signals that make up our data.
So what do we see? Well it certainly seems like W×H very closely approximates our data:
But matrix H is not full of 0s and 1s. It seems to be full of numbers close to 0 and numbers around 0.045. This is because there are many ways to factor a number, i.e. 0.5 × 8 = 4, just like 2 × 2 does. And in this case, the NMF algorithm had no idea that we expected matrix H to be 0s and 1s, so it did the best it could. For a similar reason, the values in matrix W seem too large. However, this is easy to fix: we simply scale matrix H by dividing it by its maximum value, and scale matrix W by multiplying it by the same value. And lo and behold, the columns of W now contain the estimate of the output of each factory and columns of H tells us on which days each factory dumped.
max(H(:))
ans =
0.0507
% This isn't good
scale_factor = max(H(:));
H = H./scale_factor;
W = W.*scale_factor;
h3 = figure();
set(h3, 'MenuBar', 'none');
set(h3, 'ToolBar', 'none');
plot(W, 'Color', [0.4 0.4 0.7], 'LineWidth', 2)
hold on
plot(allfactories, 'Color', [0.7 0.4 0.4], 'LineWidth', 2)
xlabel('Time (hour)')
ylabel('Contaminant amount')
legend('Original Factory Ouput','','', 'NMF Approximation','','');
You can see that the approximation isn’t perfect, we could improve that possibly by running the nnmf() function with more replicates, by allowing it more iterations before it terminates and certainly by collecting more data. But nonetheless, I hope you see the importance of what has just happened, with nothing more than the raw data, an assumption that the data was a sum of positive signals, and the knowledge of how many signals there are, NMF has almost perfectly pulled apart those signals.
Example 2 – Calcium Imaging
I wont bore you with the code, but I made a model of some calcium imaging data, where I have 5 cells glowing, and their brightness changes over time. Like this:

Conceptually, you should be able to see how each frame of this video is basically a sum of the activity of these five cells. So we should be able to use NMF to factorize this data into a W matrix that contains a picture of each cell, and an H matrix that contains information related to how bright each cell is in time. However, there is a complication. Like any normal person would, I have stored this movie as a [height] x [width] x [number of frames] matrix, i.e. a 3D matrix. NMF only works on 2D matrices. So what do we do? Well have have to reshape our movie so that each column is one frame, and each row is a particular pixel, i.e. the first column is the first frame, and the first row is the top left pixel, like this:
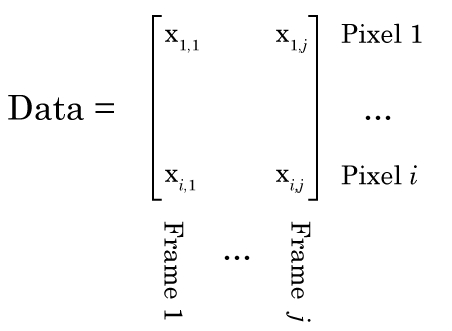
Once we’ve done that, NMF should be able to factorize the matrix like this:
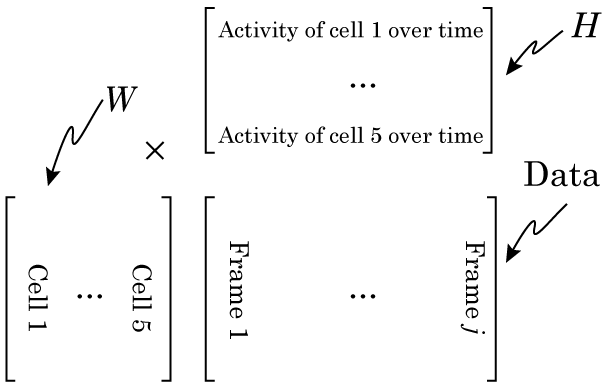
This may seem a bit hard to grasp at first, but go back to the factory example: there, each column of W was the output of each factory, and H told us if the factory was active or not. This is very similar, W is the “shape” of each cell, and H tells us how active that cell is. After we run NMF, we simply reshape each column of W back into a height x width matrix to see each cell, and we plot each row of H to see how active it is.
So when we run the NMF on that movie above, we can extract the following data: the images on the left are the reshaped columns of matrix W, and the graphs on the right are the rows of matrix H (again, I had to apply some scaling factor to W and H).
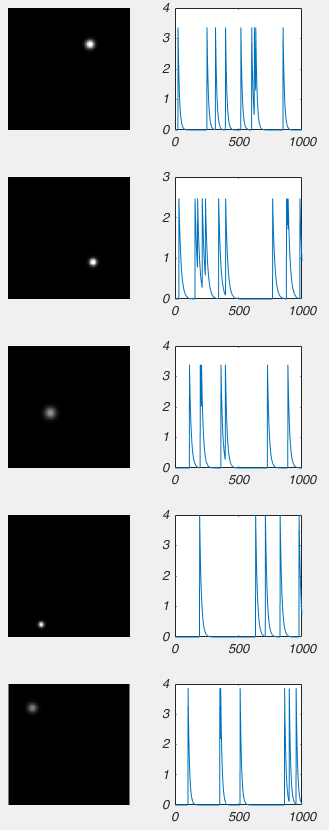
Now while I’m not suggesting that everyone drops their hand drawn ROIs just yet, you’ve got to admit that one line of matlab code achieving that is impressive. If you want to have a go yourself, the script is available here.
Example 3 – Faces
So now we’re going to do something weird. We’re going to try to factorize faces. You can kinda see how a face can be seen as a sum of different parts, e.g. eyes, noses, mouth. We have a dataset here called the “Frey Faces” which are 2000 images of Prof. Brendan Frey making faces at a camera.

After some thought, you should be able to see that NMF is unlikely to pull out images of eyes, noses etc, because every image contains eyes, noses etc, i.e. these aren’t the individual signals that are summed to make each photo. What changes are the expressions. So what we should pull out are the signals that vary with each expression. It’s also worth pointing out that, unlike the 3 factory or 5 cell example, in this data set, we don’t know the number of individual signals. But have a quick look at the dataset, I’m going to say there are 8 primary facial expressions. Like always, we need to organize our data, in this case so that each column represents one face, and each row represents a given pixel. Running the NMF, and then reshaping the columns of W back to the right size shows us the supposed individual signals that make up the total.

Some of these individual signals seem believable, others a little strange, but lets roughly gauge how well we did by comparing the original faces to those reconstructed when we multiply H by W.

I believe it is fair to say that these are convincing, though not perfect, estimates of the original.
Obviously, there is no scientific breakthrough here. But I just wanted to show how varied applications of NMF can be.
Summary
So NMF is a technique that splits your data up into a set of individual signals and weights to apply to those signals to recreate your original data. It works best when your data is truly a sum of individual signals (e.g. the factory and calcium imaging examples) but it will still work to some degree when the data isn’t quite like that (the faces). There are some caveats when it comes to applying NMF that I have mentioned (e.g. the data needs to be positive, and laid out in an appropriate matrix) but a variety I haven’t mentioned (what is the relationship between the number of observations/columns in the data matrix and the number of individual signals you can decompose the data into?). But this wasn’t meant to be a comprehensive discussion of NMF, just something to get you started.
If you want to see some published application of NMF and to make it clear that I don’t think I’m the first person to invent the idea of using NMF to probe calcium imaging data or faces, have a look at this paper “Simultaneous Denoising, Deconvolution, and Demixing of Calcium Imaging Data” from the Paninski lab or “Learning the parts of objects by non-negative matrix factorization” from Lee & Seung.
]]>What is a filter?
Fig 1. On the left is a recording from a neuron shown in the “time domain”. The two graphs on the right show the same recording in the “frequency domain”
Fig 2. A graph of Y = sin(2π X) and a graph of Y = sin(2πX + π/2) have the same frequency components, but different phases
There are a huge variety of filters, but one of the simplest ways of dividing them up is to consider what signals they don’t affect, i.e. what signals they let pass through them. So a low-pass filter lets through low frequency signals and a high-pass filter lets through high frequency data. There are also band-pass filters which only let through signals in a particular frequency range and to break convention, band-stop filters, which stop signals inside a particular frequency range. The frequency at which the signal begins to be filtered is called the “corner frequency” or the “cut-off frequency”. When we describe the actions of a filter, we are often show it’s frequency response, which is shows you what the filter does to various frequency components of your data. This can be estimated by applying the filter to your data, viewing it in the frequency domain and then dividing that by your original signal in the frequency domain. However, as your data doesn’t usually contain all frequency components, it better to create white noise, which is a signal that has the same amount of power in all frequency components. We can convert data to the frequency domain by using the Fourier transform (which I’ve talked about before here). In code, that looks like this.
signal = randn(1000,1); %Create white noise
dt = 0.5; %dt is the time between samples
time = 1:dt:1000 ; %create time base
%% Filter the data
%Make a simple running average filter
%Take the mean of the original data in a window
%of the data tempC(i:i+window)
%I know there are faster ways of doing this.
tempC_filt = zeros(size(signal));
window = 5;
for i = 1:length(signal)
end_idx = i+window;
if end_idx > length(signal)
end_idx = length(signal);
end
tempC_filt(i) = mean(signal(i:end_idx));
end
%% Now convert data to frequency domain
nfft = 2^nextpow2(length(signal)); %FFTs are faster if you perform them
%on power of 2 lengths vectors
f = (1/dt)/2*linspace(0,1,nfft/2+1)'; %Create Frequency vector'
dft = fft(signal, nfft)/(length(signal)/2); % take the FFT of original
dft_filt = fft(tempC_filt, nfft)/(length(tempC_filt)/2); %take FFT of filters
mag = abs(dft(1:nfft/2+1)); %Calculate magnitude
mag_filt = abs(dft_filt(1:nfft/2+1)); %Calculate magnitude
loglog(f, mag_filt./mag)
xlabel('Frequency (Hz)')
ylabel('Signal Out / Signal In')
The above code produces the graph in figure 3, which shows the the frequency components of the filtered signal divided by the frequency component of the original signal. What it shows us is that the running average filter doesn’t affect signals below 10^-1 Hz (0.1 Hz), but attenuates them above that. It also shows us that a running average filter doesn’t uniformly attenuation signals above 0.1 Hz, but instead filters out signals more strongly at about 0.4 Hz and 0.8 Hz than it does at 0.6 Hz and 1 Hz. This problem is refereed to as “ripples in the stop band”, where the “stop band” is the region of frequencies where the signal is attenuated, and “ripples” are the changing amount of attenuation of your signal with frequency. Compare this the “perfect” filter, where the signal is not attenuated at all up until some frequency, and then the signal is completely obliterated beyond that (I know it’s shown as only being attenuated by 10^-3, but you can’t show 0 on a log axis). This “perfect” filter is what most filters want to be. They want to not alter the signal in frequency ranges of the “pass band”, and completely remove the signal in the stop band. But filters like that are impossible to create in real life.
Now I’ve said a perfect filter doesn’t want to alter signals in the pass-band, and by looking at the graph above, it might appear that so long as you are below about 0.1 Hz you wont affect the signal, but as I alluded to before, we need to consider what the filter does to the phase. We can achieve that by adding only a few more lines to our above code.
signal = randn(1000,1); %Create random time series data
dt = 0.5; %dt is the time between samples
time = 1:dt:1000 ; %create time base
%% Filter the data
%Make a simple running average filter
%Take the mean of the original data in a window
%of the data tempC(i:i+window)
%I know there are faster ways of doing this.
tempC_filt = zeros(size(signal));
window = 5;
for i = 1:length(signal)
end_idx = i+window;
if end_idx > length(signal)
end_idx = length(signal);
end
tempC_filt(i) = mean(signal(i:end_idx));
end
%% Now convert data to frequency domain
nfft = 2^nextpow2(length(signal)); %FFTs are faster if you perform them
%on power of 2 lengths vectors
f = (1/dt)/2*linspace(0,1,nfft/2+1)'; %Create Frequency vector'
dft = fft(signal, nfft)/(length(signal)/2); % take the FFT of original
dft_filt = fft(tempC_filt, nfft)/(length(tempC_filt)/2); %take FFT of filters
mag = abs(dft(1:nfft/2+1)); %Calculate magnitude
mag_filt = abs(dft_filt(1:nfft/2+1)); %Calculate magnitude
phase = angle(dft(1:nfft/2+1));
phase_filt = angle(dft_filt(1:nfft/2+1));
%% Create an ideal filter frequency response
mag_perf = ones(size(mag_filt));
mag_perf(100:end) = 10^-3;
subplot(1,2,1)
loglog(f, mag_filt./mag, f, mag_perf)
xlabel('Frequency (Hz)')
ylabel('Signal Out / Signal In')
legend('Running Average Filter', 'Perfect Filter')
subplot(1,2,2)
semilogx(f, unwrap(phase-phase_filt));
xlabel('Frequency (Hz)')
ylabel('Phase Shift (Rad)')
Here we can clearly see that the phase of the signal is being affected at frequencies as low as 0.05 Hz. So while the amplitude of these frequency components isn’t being changed, they are being shifted later in time. So this is not a particularly good filter. Let’s move on in our quest to both understand, and create a better filter.
Filter Poles
(From here on in, I’m only going to be talking about low-pass filters, as everyone uses them. But everything I say is applicable to high-pass filters too)Another way of describing a filter is by the number of “poles” it has. I’m not going to explain to you what a pole is, because it comes from the mathematical analysis of filters, and ultimately, it is irrelevant for understanding what the consequence of the filter is. Simply put a filter with more poles attenuates frequencies more heavily for each Hz you go up. Here a figure will paint a thousand words, so see fig 5. We can create that figure with the below code.
%All our filters will have a corner
%frequence (fc) of 1000 Hz
fc = 1000; % Corner Frequency of
[b2pole,a2pole] = butter(2,2*pi*fc,'s'); %Create a 2 pole butterworth filter
[h2pole,freq2] = freqs(b2pole,a2pole,4096); %Calculate Frequency Response
[b6pole,a6pole] = butter(6,2*pi*fc,'s'); %Create a 2 pole butterworth filter
[h6pole,freq6] = freqs(b6pole,a6pole,4096); %Calculate Frequency Response
%Plot frequency response
loglog(freq2/(2*pi),abs(h2pole));
hold on
loglog(freq6/(2*pi),abs(h6pole));
xlabel('Frequency (Hz)');
ylabel('Magnitude');
legend('2 Pole Butterworth', '6 Pole Butterworth')
As you can see, as we increase the number of poles in our filter the closer it gets to our perfect filter. Or in electronic engineering terms, it has a steeper “roll off”. You might ask “well then why don’t we use 1 million pole filters then?”. Well digitally, we can create very high order filters. However, when it comes to real circuits there are a bunch of reasons why this is difficult, one of which is that it becomes very difficult to find resistors and capacitors of the exact correct value needed. Another reason is that by the time you get up to 8 poles, that is usually good enough. For instance, with an 8 pole Butterworth filter, you attenuate a signal at twice the corner frequency to about 4% of it’s original value. At 10x the corner frequency, the signal is attenuated by about 1 billion fold. But the important thing to note is that even with a filter with a large number of poles it does not remove ALL of the signal above the corner frequency.
Butterworth?
%All our filters will have a corner
%frequence (fc) of 1000 Hz
fc = 1000; % Corner Frequency of
n_poles = 8;
[zbess, pbess, kbess] = besself(n_poles, 2*pi*fc); %Create 8 pole Bessel
[bbess,abess] = zp2tf(zbess,pbess,kbess); %Convert to transfer function
[hbess,freqbess] = freqs(bbess,abess,4096); %Calculate Frequency Response
[bbut,abut] = butter(n_poles,2*pi*fc,'s'); %Create a 8 butterworth filter
[hbut,freqbut] = freqs(bbut,abut,4096); %Calculate Frequency Response
[bcheb,acheb] = cheby1(n_poles,3,2*pi*fc,'s'); %Create 8 pole Chebychev cheby1(n,3,2*pi*f,'s');
% with 3dB of ripple
[hcheb,freqcheb] = freqs(bcheb,acheb,4096); %Calculate Frequency Response
%Plot frequency response
figure;
loglog(freqbess/(2*pi), abs(hbess))
hold on
loglog(freqbut/(2*pi),abs(hbut));
loglog(freqcheb/(2*pi),abs(hcheb));
xlabel('Frequency (Hz)');
ylabel('Magnitude');
legend('Bessel', 'Butterworth', 'Chebychev')
xlim([10 10000])
ylim([10^-4 2])
However, when comparing the Bessel and the Butterworth, it may seem like the Butterworth is clearly superior: The Bessel filter attenuates signals below the corner frequency just like the Chebyshev! But when you look in the time domain, the reason why physiologists nearly always use a Bessel filter becomes obvious. Other filters producing “ringing” after encountering a step-like response. This is because the other filters delay waves of different frequencies by different times (remember, a step like response is created by a sum of a large number of waves). However, the Bessel filter doesn’t do this. The technical way to describe this is that a Bessel filter has linear phase response. This doesn’t mean it affects the phase of all the frequencies in the pass band equally, but that the way if shifts the phase means that the various frequency components aren’t shifted in time by different amounts (think about the fact that one cycle of a slow wave lasts for longer than a faster wave, so if both waves were shifted by half a wave, then slow wave would be shifted by more time). It turns out the Bessel filter is the best possible way to achieve this.
Digitizing – The hidden filter
%% Original, high sample rate signal
% Let us imagine this is like our analog signal
nfft = 4096;
dt = 0.001; % inter sample time = 0.001s = 1kHz sampling
t = (1:nfft)*0.001; % time vector
% Create signal vector that is the sum of 32 Hz, 64 Hz, and 256 Hz
signal = sin(32*2*pi*t) + sin(2*pi*64*t) + sin(2*pi*256*t);
f = (1/dt)/2*linspace(0,1,nfft/2+1)'; %Create Frequency vector
dft = fft(signal, nfft)/(length(signal)/2); % take the FFT of original
mag = abs(dft(1:nfft/2+1)); %Calculate magnitude
semilogx(f, mag, 'LineWidth', 2 );
%% Now lets digitize our faux-analog signal
% Essentially we are down sampling,
% by sampling it every 0.005s = 200 Hz = every 5th sample.
signal_dig = signal(1:5:end);
nfft_dig = 2^nextpow2(length(signal_dig)); %FFTs are faster if you perform them
%on power of 2 lengths vectors
f_dig = (1/(dt*5))/2*linspace(0,1,nfft_dig/2+1)'; %Create Frequency vector
dft_dig = fft(signal_dig, nfft_dig)/(length(signal_dig)/2);
mag_dig = abs(dft_dig(1:nfft_dig/2+1));
hold on
semilogx(f_dig, mag_dig, 'LineWidth', 2);
xlim([10 1000])
xlabel('Frequency (Hz)');
ylabel('Magnitude');
legend('Original Signal', 'Digitized Signal');
In the code, we create a signal that is a sum of 32, 64 and 256 Hz sine waves. We’ll think of this signal as being our analog signal. We then “digitize” it as 200 Hz. We then look at the two signals in the frequency domain. In the original signal we see peaks at 32, 64 and 256 Hz, and after we digitize it at 200 Hz, we see a loss of 256 Hz signal, which perhaps isn’t too surprising when you think about it. But something very disturbing has happened, we now have a new signal with a peak at 56 Hz. This signal is a complete phantom and is called “Aliasing”, and it happened because we need to filter before we digitize (See Fig 9B). This is a correlate of the Nyquist-Shannon sampling theorem, which says that any signal which has no frequency component higher than F, can be perfectly reconstructed if it is sampled at 2F. So, inversely, if we digitize a signal at rate 2F, but it has frequency components higher than F, then the digitized signal we end up with is not a faithful representation of the original. Now let’s try to follow the rules. If we add in these lines of code, then we get Fig 9A.
%% Let's filter the signal before we digitize it [bbut,abut] = butter(8,100/(1000/2)); %Create a 100Hz, 8 pole butterworth filter signal_filt = filter(bbut, abut, signal); %Filter the data signal_filt_dig = signal_filt(1:5:end); dft_filt_dig = fft(signal_filt_dig, nfft_dig)/(length(signal_filt_dig)/2); mag_filt_dig = abs(dft_filt_dig(1:nfft_dig/2+1)); semilogx(f_dig, mag_filt_dig, 'LineWidth', 2);
And this is one of the two reasons why we must ALWAYS low-pass filter data before we digitize it: if we don’t, we will get aliases, i.e. spurious frequency components. This is also what causes strange patterns in some photographs, the original data had higher frequencies (i.e. patterns changing in space) than the camera CCD could sample. The other reason we filter BEFORE was digitize is that high frequency noise can sometimes be larger than the signal we want to record, and hence filtering before digitization allows us to amplify the signal as much as possible without saturating the digitizer.
Choosing a corner and sampling frequency
dt = 1/20000; % 20kHz sampling rate
t = 0:dt:0.02; % time vector 4ms long
signal = exp(-(t-0.01).^2/(0.001/sqrt(2*log(2)))^2); %Gaussian with 1ms FWHM
nfft = 2^nextpow2(length(signal)); %FFTs are faster if you perform them
%on power of 2 lengths vectors
f = (1/dt)/2*linspace(0,1,nfft/2+1)'; %Create Frequency vector
dft = fft(signal, nfft)/(length(signal)/2); %take the FFT of original
mag = abs(dft(1:nfft/2+1)); %Calculate magnitude
subplot(1,2,1);
semilogx(f, mag, 'LineWidth', 2);
title('Freq Components of Original')
xlabel('Frequency (Hz)');
ylabel('Magnitude');
xlim([30 10000]);
xticks([100, 1000, 10000]);
[bbess, abess] = besself(8, 2*pi*1000); %Create 8 pole 1kHz filter
[num,den] = bilinear(bbess,abess,1/dt);
signalbess1k = filter(num, den, signal); %Apply Filter
[bbess, abess] = besself(8, 2*pi*5000); %Create 8-pole 5kHz filter
[num,den] = bilinear(bbess,abess,1/dt);
signalbess5k = filter(num, den, signal); %Apply Filter
subplot(1,2,2);
plot(t*1000,signal, t*1000, signalbess1k, t*1000, signalbess5k, 'LineWidth', 2);
xlabel('Time (ms)')
ylabel('Amplitude')
legend('Original Signal', 'Filtered Signal (1kHz)', 'Filtered Signal (5kHz)', 'Location', 'south');
I should probably add that these rules of thumb are not absolute (apart from digitizing at greater than twice your filter rate: always do that!). If your filter slightly deforms the shape of your action potential, or slightly delays it in time, this may not matter for your particular experiments. But you should still be aware of the fact that if you’re filtering too close to your signal of interest, you are not recording the “true” signal.
Conclusion/Rules of Thumb
- A filter removes unwanted frequeny components
- A low-pass filter removes high frequency signals
- A filter with more poles has a steeper roll off
- A Bessel filter has the best behaviour in the time domain
- For a 4-pole Bessel, you must filter at at least 4 times the frequency of the fastest wanted component of your signal
- For an 8-pole Bessel, you must filter at at least 5 times the frequency of the fastest wanted component of your signal
- You must digitize at more than 2-3 times the frequency of your low-pass filter
Stimulus Isolators can be split up it two ways: the first way is battery powered versus mains powered, and the second way is constant current versus constant voltage. For the discussion today, it makes no difference. In both constant voltage and constant current stimulators, a voltage drives current between the two output terminals of the stimulator. And mains powered stimulus isolators try their very best to approximate battery powered stimulus isolators by running the AC voltages from the mains through some kind of transformer, which effectively “isolates” the stimulus isolator from earth. What do I mean what I say “isolates”? I mean that if a power source is isolated from earth, then the output of that power source cannot be measured relative to earth, as no current wants to flow from the power output to earth. Still confused? Let’s look at Fig. 1.
Here we have a 9 volt battery, which truly has 9 volts between it’s positive and negative terminals. We get a multimeter and put it’s red lead on the positive terminal, and connect the black lead to earth. What voltage do we see on the multimeter? We see zero volts. We can explain this in lots of ways, but the simplest is to remember that current must flow in a circuit, in order for the multimeter to sense the voltage on the battery, electrons must flow from the battery to the earth, which if it did, it would not be able to get back to the negative terminal of the battery. Another way of thinking about this is that the multimeter is asking a question something like “What is the a height difference between the peak of Mount Everest (on Earth) and the peak of Mount Olympus (on Mars)?”. Yes, you could measure the height of each mountain from sea level (equivalent to measuring the voltage difference between ground and ground (0V) and the voltage difference between then positive and negative terminals of the battery (9V)) and then compare that measurement, but that isn’t what the question was. Directly asking what the the height difference between the peaks doesn’t even really make sense as a question because they share no common reference point. Similarly, asking what voltage exists between a battery terminal and the earth makes no sense unless the battery connected to earth, like it is in Fig 2. Now current can happily flow from the positive terminal of the battery, into the multimeter, into ground and then back into the battery. Or to put it another way, now the battery and the multimeter have a common reference point: the ground.So what does this have to do with stimulus isolators? Well if we replace the battery with a stimulus isolator, and the multimeter with our electrode connected to a preamplifier, we have a typical electrophysiology set up. If our stimulator is not isolated from ground, then the voltage it creates will be directly sensed by our preamplifier. How does this work? Well have a look at Fig 3.
Fig 3. shows us a non-isolated stimulator. I’ve drawn it’s power supply as a battery, but it could as well be a voltage output from a DAC or any other non-isolated voltage. Our recording electrode is sampling the voltage at VRecord, which is the same place as the two electrodes of our bipolar stimulating electrode (yes, there will be some resistance between all of these, but they don’t really matter in order to get a conceptual understanding).
Now you may be saying “Hang on there, I’ve used a stimulus isolator before, and I still see a stimulus artifact”, and of course, you do. This is because while a good stimulus isolator is essentially completely isolated from ground, resistively speaking, it still has some capacitive coupling to ground, usually on the order of 1-10’s of pF. So this is like putting a capacitor between the battery and ground in Fig 3. What this means is that rapidly changing voltages caused by your stimulator still allow some current to flow through RGround, creating a small stimulus artifact, but the smaller this capacitive coupling is, this smaller and briefer the artifact will be.
So what does this mean? It means don’t ground either of the output pins of your stimulator or you will undo all the engineering that has gone into the design of your stimulator! It means don’t let the leads which run to your stimulator run all over your rig (which increases the capacitive coupling to ground). While I’ve found wrapping your stimulator leads in a grounded shield (or using coaxial cables with a grounded shield) is a good way to remove high frequency noise introduced by the stimulator (or more the leads attached to the stimulator acting like antennas), it also can increase the capacitive coupling to ground, so you get a bigger artifact.
There is another benefit of using stimulus isolators: safety. Specifically, if you were to hold onto the positive output of a non-isolated 100V stimulator, it wouldn’t be fun, as current could flow through you, into ground, and from ground, back to the stimulator. However, if this stimulator was isolated this couldn’t happen, as there is no return path from ground to the stimulator. It’s basically the inverse of why birds can sit on overhead cables carrying mains electricity: the bird is isolated from ground, while the power isn’t, in our case however, it is the power which is isolated from ground, while you aren’t. In practice, if your are an in vitro scientist, this is a pretty theoretically benefit, but if you are using stimulators in a clinical setting to excite nerves or muscles, this is very important, as the last thing you want is current to flow through your patients heart to ground: you only want the current to flow between the two poles of your stimulating electrodes and into the muscle/nerve of choice.
]]>The main script is available here, and it requires distinguishable_colors.m (which in turn requires the image processing toolbox I believe).
The code is relatively well documented/commented, and there is even a ‘Help!’ button. If anyone has any problems with it, please let me know.
]]>